
Читайте также:
|
Из уравнения (6.99) следует, что для функции реакции с положительным наклоном существует «мультипликатор», усиливающий эффект сдвига функции реакции для данного уровня 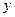 , т.е.
, т.е.  . Это также видно на диаграмме: воздействие на равновесный уровень
. Это также видно на диаграмме: воздействие на равновесный уровень 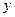 является большим, чем просто величина сдвига вверх функции реакции. И чем ближе наклон функции реакции к 1, тем сильнее будет данный эффект мультипликатора.
является большим, чем просто величина сдвига вверх функции реакции. И чем ближе наклон функции реакции к 1, тем сильнее будет данный эффект мультипликатора.
В данной ситуации любой фактор, оказывающий воздействие на функцию реакции, будет иметь еще больший эффект на общий уровень экономической активности. В терминологии Саммерса (Summers, 1988), равновесие является хрупким. Таким образом, возможно, что существует значительная реальная жесткость, но при этом экономические колебания определяются не номинальными, а реальными шоками. Технологические шоки, дезинтеграция на рынке кредита, изменения в государственных расходах и ставках налогов, рост или снижение неопределенности относительно будущей политики, и другие реальные шоки – все это может быть важным источником колебаний выпуска в случае, когда имеет место высокая степень реальной жесткости. Как мы видели, вряд ли существенная реальная жесткость может иметь место в вальрасовской модели. Поэтому, теории колебаний, основанные на реальной жесткости и реальных шоках, называются реальными невальрасовскими теориями. И коль скоро существует много потенциальных источников реальной жесткости, существует довольно много теорий данного типа.[42]
В действительности, для объяснения экономических колебаний не столь важно, существует ли множество равновесий с гибкими ценами, или единственное, но хрупкое равновесие. Предположим, как мы делали это на протяжении всего данного раздела, что на пути номинальной подстройки цен нет никаких препятствий. Если в экономике существует множество равновесий, то колебания могут возникнуть в отсутствии каких-либо шоков. При этом экономика перемещается из одного равновесия в другое. С другой стороны, если равновесие является единственным, но хрупким, колебания могут быть спровоцированы незначительными шоками, т.к. на равновесие в данном случае будет оказываться намного большее воздействие.
Ситуация является схожей и в случае существования небольших барьеров на пути подстройки цен. Высокая степень реальной жесткости (плюс соответствующая нечувствительность прибыли) снижает стимул фирмы подстраивать свою цену в ответ на номинальные шоки. При этом не так уж и важно, является ли степень реальной жесткости настолько высокой, чтобы породить множество равновесий с гибкими ценами.
Ограничения
Кейнсианская теория содержит широкий класс моделей, большинство из которых нацелены скорее на определенные узкие вопросы, и не пытаются дать всеобъемлющее описание экономики. Кроме того, кейнсианский подход к колебаниям часто отводит важную роль разнообразным типам шоков и рыночных несовершенств.
Данные черты кейнсианского подхода создают основу для многочисленной критики: кейнсианские модели являются настольно расплывчатыми и гибкими, что их практически невозможно проверить на состоятельность. Также как последователи Птолемея готовы были объяснить любое новое наблюдение с помощью эпициклов, кейнсианские макроэкономисты могут модифицировать любую из своих теорий и постулировать ненаблюдаемые шоки для того, чтобы подвести статистику под практически любую ситуацию.
Несложно указать на примеры гибкости кейнсианского анализа, начиная с общих предположений моделей и заканчивая спецификой индивидуальных эпизодов. Вскоре после публикации Общей Теории, в работе Dunlop (1938) были представлены убедительные доказательства против ее предсказаний относительно контрциклического характера реальной заработной платы. Но вместо того, чтобы отказаться от своей теории, Кейнс (Keynes, 1939) просто отметил необходимость изменения предположений о характере ценообразования. Другой пример: ответ кейнсианской школы на нарушение тесной взаимосвязи между выпуском и инфляцией в конце 1960-ых – начале 1970-ых состоял в модификации моделей, включение в них шоков предложения и базовой инфляции. Аналогично, получив убедительные доводы в пользу того, что микроэкономические процессы подстройки номинальных цен не могут быть объяснены одними лишь небольшими фиксированными издержками изменения цен, новые кейнсианцы не отказались от своих теорий. Они просто согласились с тем, что в реальности препятствия на пути номинальной подстройки представлены сложной комбинацией издержек подстройки и других факторов (D. Romer, 1993), и что издержки меню – это всего лишь метафора, имеющая такое же отношение к реальности, как и вальрасовский аукционер в моделях конкуренции (Ball and Mankiw, 1994). И далее в том же духе.
Такая же гибкость характеризует не только кейнсианские модели, но и кейнсианский подход к частным эпизодам. Модели допускают возможность шоков в любых секторах экономики, будь то шоки предложения денег и спроса на деньги, шоки фискальной политики, шоки потребления и инвестиций, шоки в установлении цен и заработной платы, шоки международной торговли. А раз так, то модели допускают почти что любые одновременные изменения в различных переменных. Например, общепринятое кейнсианское объяснение рецессии в США в 1981-1982 годах состоит в том, что она была спровоцирована жесткой монетарной политикой. И тот факт, что в этот период не наблюдалось значительного снижения темпа роста денежной массы, вовсе не воспринимается как серьезное противоречие: дополнительно постулируется сдвиг спроса на деньги, к которому Федеральная Резервная Система подстроилась лишь частично. Подобным же образом кейнсианцы объясняют и рецессию в США в 1990-1991 годах. В данном случае речь идет о непонятном снижении степени «доверия потребителей». А совпадение во времени во второй половине 1990-ых высокого темпа роста выпуска и очень низкой безработицы со стационарной или снижающейся инфляцией приписывается, в основном, благоприятным шокам предложения и снижению естественного уровня безработицы. В действительности, это просто вытекает из самой динамики рассматриваемых макроэкономических переменных.
Возможно, что экономика является сложной, что существует много разных типов шоков, и что модификация кейнсианских моделей отражает поступательный прогресс в понимании экономических процессов. Но теория, которая является настолько гибкой, что не входит в противоречие ни с какими наблюдениями, лишена смысла. Таким образом, для того, чтобы кейнсианская теория была полезной, должны находится такие вопросы, на которые она давала бы четкий ответ.
Одна из проблем, относительно которой кейнсианская теория дает четкое представление - это реальные эффекты номинальных шоков. Основной элемент всех кейнсианских моделей – это отсутствие мгновенной подстройки номинальных цен и заработной платы. В результате, модель предсказывает, что независимые монетарные шоки должны воздействовать на реальную экономическую активность. Если бы данное предсказание противоречило наблюдениям, то от подобных моделей пришлось бы отказаться вовсе, а не пытаться их модифицировать. И это означало бы необходимость исследовать колебания на основе моделей реального делового цикла из главы 4 или на основе реальных невальрасовских теорий из предшествующего раздела. И напротив, если верен вывод из раздела 5.5 о том, что монетарные шоки имеют важные реальные эффекты, то теории колебаний должны содержать в себе важный кейнсианский элемент. Но даже в этом случае было бы желательно усовершенствовать и четче очертить границы кейнсианской теории там, где она дает более сильные и четкие предсказания.
Задачи
6.1. Рассмотрим проблему, с которой сталкивается индивид в модели Лукаса в ситуации, когда 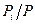 неизвестно. Индивид выбирает
неизвестно. Индивид выбирает 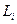 , максимизирующее ожидания
, максимизирующее ожидания 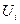 . При этом
. При этом 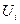 по-прежнему задается уравнением (6.3).
по-прежнему задается уравнением (6.3).
(a) Найдите условие первого порядка для 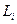 и преобразуйте так, чтобы получить зависимость
и преобразуйте так, чтобы получить зависимость 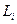 от
от 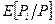 . Прологарифмируйте полученное выражение, чтобы найти выражение для
. Прологарифмируйте полученное выражение, чтобы найти выражение для  .
.
(b) Как соотносится объем предложения труда индивида в ситуации, когда его поведение соответствует принципу эквивалентности детерминированному случаю (6.17), с оптимальным значением, найденным в пункте (а)? (Подсказка: как 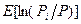 соотносится с
соотносится с 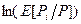 ?)
?)
(c) Предположим (как и в модели Лукаса), что 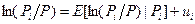 , где
, где 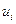 распределено нормально со средним значением 0 и дисперсией, независящей от
распределено нормально со средним значением 0 и дисперсией, независящей от  . Покажите, что при этом выполняется условие
. Покажите, что при этом выполняется условие 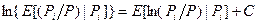 , где
, где 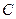 - это константа, значение которой не зависит от
- это константа, значение которой не зависит от  . (Подсказка: обратите внимание на то, что
. (Подсказка: обратите внимание на то, что  и покажите, что из этого следует, что
и покажите, что из этого следует, что  , максимизирующее ожидаемую полезность, отличается от принципа эквивалентности (6.17) только на константу.)
, максимизирующее ожидаемую полезность, отличается от принципа эквивалентности (6.17) только на константу.)
6.2. (На основе Dixit and Stiglitz, 1977.) Предположим, что индекс потребления  в уравнении (6.2) задается следующим образом:
в уравнении (6.2) задается следующим образом: 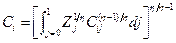 , где
, где 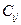 – это потребление индивидом блага
– это потребление индивидом блага 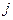 , и
, и 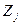 – это шок предпочтений относительно блага
– это шок предпочтений относительно блага 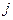 . Предположим, индивид может потратить на покупку благ сумму
. Предположим, индивид может потратить на покупку благ сумму  . Таким образом, бюджетное ограничение имеет вид
. Таким образом, бюджетное ограничение имеет вид  .
.
(a) Найдите условие первого порядка в задаче максимизации  для данного бюджетного ограничения. Выразите
для данного бюджетного ограничения. Выразите 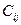 через
через 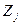 ,
, 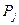 и множитель Лагранжа для бюджетного ограничения.
и множитель Лагранжа для бюджетного ограничения.
(b) Используя бюджетное ограничение, найдите выражение для 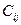 через
через 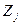 ,
, 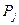 ,
,  , и прочие
, и прочие 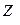 и
и  .
.
(c) Подставьте полученный в пункте (b) результат в выражение для  и покажите, что
и покажите, что 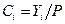 , где
, где 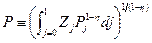 .
.
(d) Используя результаты пунктов (b) и (c) покажите, что 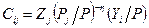 .
.
(e) Сравните полученные результаты с выражениями (6.7) и (6.9).
6.3. Эмпирическая эквивалентность. (Sargent, 1976.) Предположим, что предложение денег определяется процессом 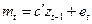 , где
, где 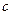 и
и  - векторы и
- векторы и 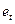 - независимо одинаково распределенная случайная величина, которая не коррелированна с
- независимо одинаково распределенная случайная величина, которая не коррелированна с  . Случайная величина
. Случайная величина 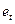 является непредсказуемой и ненаблюдаемой. Таким образом,
является непредсказуемой и ненаблюдаемой. Таким образом, 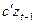 - ожидаемая компонента
- ожидаемая компонента 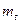 , а
, а 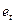 - неожидаемая компонента
- неожидаемая компонента 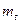 . Определяя предложение денег, Федеральная Резервная Система реагирует только на переменные, которые влияют на реальную активность. Т.е., предполагается, что переменные в векторе
. Определяя предложение денег, Федеральная Резервная Система реагирует только на переменные, которые влияют на реальную активность. Т.е., предполагается, что переменные в векторе  непосредственно воздействуют на
непосредственно воздействуют на 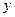 .
.
Рассмотрим две возможные модели. (i) Только ожидаемая компонента денежного предложения имеет значение, т.е. 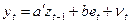 . (ii) Все компоненты денежного предложения имеют значение, т.е.
. (ii) Все компоненты денежного предложения имеют значение, т.е. 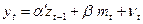 . В каждой модели предполагается, что шоки имеют независимое одинаковое распределение и не коррелированны с
. В каждой модели предполагается, что шоки имеют независимое одинаковое распределение и не коррелированны с  .
.
(a) Можно ли провести различие между двумя этими теориями? Другими словами, для данного набора параметров в модели (i), существует ли набор параметров в модели (ii), который дает тот же результат? Объясните почему.
(b) Предположим, что Федеральная Резервная Система также реагирует на некоторые переменные, не оказывающие прямого воздействия на выпуск. Т.е., предположим, что  , и рассмотрим те же две модели (i) и (ii) (полагая, что соответствующие шоки некоррелированны как с
, и рассмотрим те же две модели (i) и (ii) (полагая, что соответствующие шоки некоррелированны как с  и
и 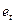 , так и с
, так и с  ). Можно ли провести различие между двумя этими теориями в данном случае? Объясните почему.
). Можно ли провести различие между двумя этими теориями в данном случае? Объясните почему.
6.4. Рассмотрим экономику, которая описывается моделью, рассмотренной в разделе 6.4. Предположим, однако, что  строится как индекс цен, введенный в части (с) задачи 6.2 (пусть при этом все
строится как индекс цен, введенный в части (с) задачи 6.2 (пусть при этом все 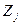 для простоты равны 1). Также предположим, что для достижения равновесия на рынке денег необходимо, чтобы совокупные расходы в экономике равнялись
для простоты равны 1). Также предположим, что для достижения равновесия на рынке денег необходимо, чтобы совокупные расходы в экономике равнялись 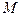 . С учетом внесенных изменений, будет ли по-прежнему равновесной ситуация, когда выпуск каждого блага определяется уравнением (6.46), а цена каждого блага – уравнением (6.47)?
. С учетом внесенных изменений, будет ли по-прежнему равновесной ситуация, когда выпуск каждого блага определяется уравнением (6.46), а цена каждого блага – уравнением (6.47)?
6.5. Индексация. (См. Gray, 1976, 1978 и Fisher, 1977b. Задача написана на основе Ball, 1988.) Предположим, что производство фирмы 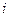 задается следующим образом
задается следующим образом  , где
, где  - это шок предложения,
- это шок предложения, 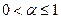 . Таким образом, в логарифмах имеем
. Таким образом, в логарифмах имеем  . Цены являются гибкими, так что
. Цены являются гибкими, так что 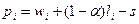 (для простоты константа нормализована к 0). Агрегирование уравнений выпуска и цен дает следующее:
(для простоты константа нормализована к 0). Агрегирование уравнений выпуска и цен дает следующее: 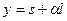 и
и  . Ставки заработной платы частично индексированы к ценам:
. Ставки заработной платы частично индексированы к ценам: 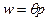 , где
, где 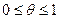 . Агрегированный спрос задается уравнением
. Агрегированный спрос задается уравнением  . При этом
. При этом 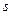 и
и  - это независимые случайные величины со средним значением 0 и дисперсиями
- это независимые случайные величины со средним значением 0 и дисперсиями  и
и 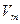 , соответственно.
, соответственно.
(a) Выпишите  ,
, 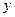 ,
,  и
и 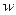 как функции от
как функции от  и
и 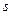 , и параметров
, и параметров  и
и 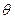 . Каким образом индексация влияет на реакцию занятости на монетарные шоки? А на шоки предложения?
. Каким образом индексация влияет на реакцию занятости на монетарные шоки? А на шоки предложения?
(b) Какое значение 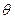 минимизирует дисперсию занятости?
минимизирует дисперсию занятости?
(c) Предположим, что спрос на продукцию одной фирмы задается уравнением  . Предположим как и прежде, что все фирмы, за исключением
. Предположим как и прежде, что все фирмы, за исключением 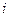 -ой фирмы, индексируют ставки заработной платы к уровню цен, т.е.
-ой фирмы, индексируют ставки заработной платы к уровню цен, т.е. 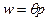 . При этом
. При этом 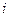 -ая фирма индексирует заработную плату к уровню цен следующим образом:
-ая фирма индексирует заработную плату к уровню цен следующим образом: 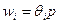 . Фирма
. Фирма 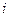 продолжает устанавливать цену на уровне
продолжает устанавливать цену на уровне 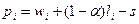 . Тогда, из производственной функции и уравнения ценообразования следует, что
. Тогда, из производственной функции и уравнения ценообразования следует, что 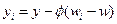 , где
, где 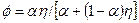 .
.
(i) Определите занятость на фирме 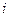 ,
,  как функцию от
как функцию от  ,
, 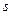 ,
,  ,
,  ,
, 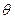 и
и  .
.
(ii) Какое значение  минимизирует дисперсию
минимизирует дисперсию  ?
?
(iii) Найдите равновесное по Нэшу значение 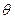 . То есть, найдите такое значение
. То есть, найдите такое значение 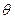 , что если агрегированное индексирование задается параметром
, что если агрегированное индексирование задается параметром 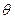 , то репрезентативная фирма минимизирует дисперсию
, то репрезентативная фирма минимизирует дисперсию  , задавая
, задавая 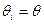 . Сравните полученное значение со значением, найденным в пункте (b).
. Сравните полученное значение со значением, найденным в пункте (b).
6.6. Синхронизированное установление цен. Рассмотрим модель Тейлора. Предположим, однако, что в каждом периоде все индивиды устанавливают цены на текущий период и на следующий. Т.е., в периоде  цены устанавливаются на периоды
цены устанавливаются на периоды  и
и  . В периоде
. В периоде  цены не устанавливаются. В периоде
цены не устанавливаются. В периоде 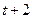 устанавливаются цены на периоды
устанавливаются цены на периоды 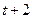 и
и 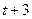 . И т.д. Как и в модели Тейлора, цены предопределены и фиксированы. Индивиды устанавливают свои цены в соответствии с (6.60). И, наконец, предположим, что
. И т.д. Как и в модели Тейлора, цены предопределены и фиксированы. Индивиды устанавливают свои цены в соответствии с (6.60). И, наконец, предположим, что  следует процессу случайного блуждания.
следует процессу случайного блуждания.
(a) Найдите цену 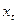 , которую в периоде
, которую в периоде  устанавливает репрезентативный индивид. Запишите
устанавливает репрезентативный индивид. Запишите 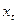 как функцию от
как функцию от 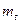 ,
, 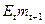 ,
, 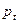 ,
, 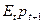 .
.
(b) Синхронизация требует, чтобы 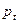 и
и 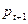 были равны
были равны 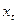 . Используя этот факт, запишите
. Используя этот факт, запишите 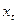 в терминах
в терминах 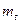 и
и 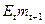 .
.
(c) Найдите величины 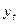 и
и  . Сохраняется ли по-прежнему основной результат модели Тейлора, что номинальные шоки продолжают воздействовать на реальные переменные даже после того, как все цены изменяются? Дайте интуитивное объяснение.
. Сохраняется ли по-прежнему основной результат модели Тейлора, что номинальные шоки продолжают воздействовать на реальные переменные даже после того, как все цены изменяются? Дайте интуитивное объяснение.
6.7. Модель Фишера с несбалансированным установлением цен. Рассмотрим экономику, моделируемую в разделе 6.5. Предположим, однако, что вместо половины индивидов, устанавливающих свои цены каждый период, доля индивидов  устанавливает свои цены в нечетные периоды, а доля
устанавливает свои цены в нечетные периоды, а доля 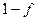 - в четные периоды. Таким образом, уровень цен равен
- в четные периоды. Таким образом, уровень цен равен  , если
, если  - четное число, и
- четное число, и 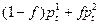 , если
, если  - нечетное число. Выведите выражения, аналогичные выражениям (6.57) и (6.58) для
- нечетное число. Выведите выражения, аналогичные выражениям (6.57) и (6.58) для 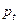 и
и 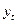 , для четного и нечетного периодов.
, для четного и нечетного периодов.
6.8. Неустойчивость постепенного установления цен. (См. Fethke and Policano, 1986; Ball and Cecchetti, 1988; Ball and D. Romer, 1989.) Рассмотрим экономику, описанную в задаче 6.7, и предположим для простоты, что  следует процессу случайного блуждания (так что
следует процессу случайного блуждания (так что 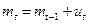 , где
, где 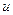 - белый шум с постоянной дисперсией). Предположим, что потери в прибыли индивида за два периода, по сравнению с ценообразованием
- белый шум с постоянной дисперсией). Предположим, что потери в прибыли индивида за два периода, по сравнению с ценообразованием 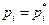 , пропорциональны
, пропорциональны 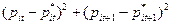 . Если
. Если  и
и 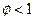 , то для кого потери в прибыли будут больше: для индивидов, устанавливающих цены в нечетные периоды, или для индивидов, устанавливающих цены в четные периоды? В свете этого, будет ли по-прежнему наблюдаться постепенное установление цен, если
, то для кого потери в прибыли будут больше: для индивидов, устанавливающих цены в нечетные периоды, или для индивидов, устанавливающих цены в четные периоды? В свете этого, будет ли по-прежнему наблюдаться постепенное установление цен, если 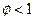 ?
?
6.9. Рассмотрим модель Тейлора в случае, когда денежная масса представляет собой белый шум, а не процесс случайного блуждания, т.е. 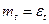 , где
, где 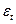 некоррелированны друг с другом. Решите модель, используя метод неопределенных коэффициентов. (Подсказка: можно ли в уравнении, аналогичном (6.63), предположить, что
некоррелированны друг с другом. Решите модель, используя метод неопределенных коэффициентов. (Подсказка: можно ли в уравнении, аналогичном (6.63), предположить, что 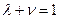 ?)
?)
6.10. Решите задачу 6.9, используя лаговые операторы.
6.11. (На основе Ball, 1994a.) Рассмотрим версию модели Тейлора в непрерывном времени, так что 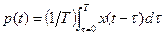 , где
, где 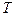 - интервал времени между изменениями цен каждого индивида, и
- интервал времени между изменениями цен каждого индивида, и 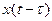 - это цена, устанавливаемая индивидами в момент времени
- это цена, устанавливаемая индивидами в момент времени 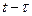 . Предположим, что
. Предположим, что 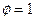 , так что
, так что 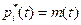 . Таким образом,
. Таким образом, 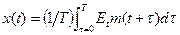 .
.
(a) Предположим, что изначально 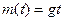 ,
,  , и, следовательно,
, и, следовательно, 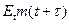 равно
равно 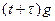 . Найдите
. Найдите 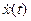 ,
,  и
и 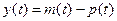 .
.
(b) Предположим, что в момент времени 0 правительство объявляет, что оно собирается монотонно снизить темп роста денежной массы до 0 на протяжении интервала времени 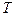 . Так что
. Так что 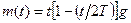 для
для  , и
, и 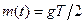 для
для  . Изменение в политике является неожиданным, поэтому цены, заданные до момента
. Изменение в политике является неожиданным, поэтому цены, заданные до момента 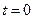 , остаются такими же, как в пункте (а).
, остаются такими же, как в пункте (а).
(i) Покажите, что если  для любого
для любого 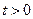 , то
, то 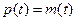 для любого
для любого 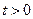 , и таким образом, выпуск будет таким же, каким бы он был без изменения в политике.
, и таким образом, выпуск будет таким же, каким бы он был без изменения в политике.
(ii) Как цены, задаваемые фирмами для периода  , будут соотноситься (больше, меньше или равны) с
, будут соотноситься (больше, меньше или равны) с 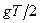 ? Что можно сказать для периода
? Что можно сказать для периода 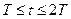 ? Каким образом выпуск в периоде
? Каким образом выпуск в периоде 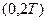 будет соотноситься с выпуском, который был бы в остутствии изменения политики?
будет соотноситься с выпуском, который был бы в остутствии изменения политики?
6.12. Определяемое состоянием ценообразование в условиях положительной и отрицательной инфляции. (На основе Caplin and Leahy, 1991). Рассмотрим модель экономики Кэплина-Спалбера. Предположим, однако, что  может, как расти, так и падать. При этом фирмы следуют двухсторонней
может, как расти, так и падать. При этом фирмы следуют двухсторонней 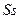 -политике: если
-политике: если 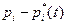 достигает
достигает  или
или 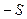 , то фирма
, то фирма 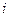 меняет цену таким образом, чтобы
меняет цену таким образом, чтобы 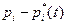 равнялось 0. Как и в модели Кэплина-Спалбера, изменения в
равнялось 0. Как и в модели Кэплина-Спалбера, изменения в  носят непрерывный характер.
носят непрерывный характер.
Предположим для простоты, что 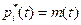 . Кроме того, предположим, что случайная величина
. Кроме того, предположим, что случайная величина 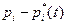 изначально распределена равномерно на некотором интервале шириной
изначально распределена равномерно на некотором интервале шириной  . Т.е., случайная величина
. Т.е., случайная величина 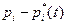 распределена равномерно на интервале
распределена равномерно на интервале 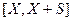 для некоторого
для некоторого 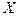 , лежащего между
, лежащего между 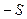 и 0. Это показано на Рис. 6.9: распределение случайной величины
и 0. Это показано на Рис. 6.9: распределение случайной величины 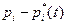 - это «лифт» высотой
- это «лифт» высотой  в «шахте» высотой
в «шахте» высотой 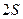 .
.
(a) Объясните, почему в данных предположениях случайная величина 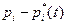 всегда будет распределена равномерно на некотором интервале шириной
всегда будет распределена равномерно на некотором интервале шириной  . (В терминах диаграммы это означает, что хотя лифт может двигать по шахте, его высота не меняется и остается равной
. (В терминах диаграммы это означает, что хотя лифт может двигать по шахте, его высота не меняется и остается равной  ).
).
(b) Существуют ли какие-либо позиции лифта (какие-либо значения 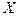 ), где предельно малое приращение в
), где предельно малое приращение в  на величину
на величину 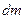 приводит к росту средних цен на величину, меньшую
приводит к росту средних цен на величину, меньшую 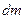 ? Большую
? Большую 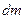 ? Равную
? Равную 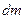 ? В соответствии с этим, что можно сказать о реальных эффектах монетарных шоков в данной модели?
? В соответствии с этим, что можно сказать о реальных эффектах монетарных шоков в данной модели?
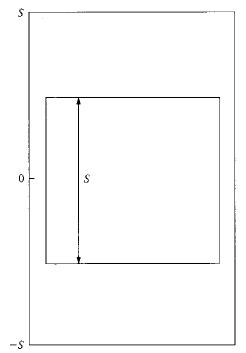
Рис. 6.9. Распределение случайной величины 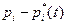
Дата добавления: 2015-10-30; просмотров: 72 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Эмпирическое приложение: экспериментальный анализ нескоординированности | | | в модели Кэплина-Лихи |