Единственное равновесие

На Рис. 6.7 представлена ситуация множества равновесий. Т.к., по предположению, функция 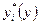лежит в пределах от 0 до , ее график должен начинаться выше линии 45 градусов, а заканчиваться соответственно ниже. И т.к. она является непрерывной, она должна пересекать линию 45 градусов нечетное число раз (если не рассматривать возможность касания). На рисунке представлена ситуация с тремя точками пересечения, т.е. с тремя равновесными значениями выпуска. Во вполне реалистичных предположениях равновесие в точке А будет неустойчивым. Например, если агенты ожидают, что выпуск будет немного выше, чем в точке А, то они в действительности произведут несколько больше, чем, как они ожидали, произведут другие. Тогда, при естественных предположениях, экономика будет удаляться от точки А. При этом равновесия в точках В и С будут устойчивыми.

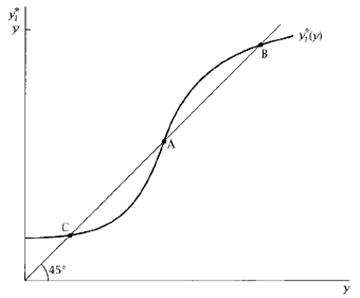
Рис. 6.7. Функция реакции, для которой существует множество равновесий

В ситуации множества равновесий фундаментальные показатели не могут полностью определить окончательное положение экономики. Если агенты ожидают, что экономика окажется в точке С, то так и произойдет. Если же они ожидают, что экономика попадет в равновесие В, то именно это и случится. Таким образом, можно говорить о том, что окончательное положение экономики будет определяться звериным инстинктом, самосбывающиеся предсказания и солнечными пятнами. [39]

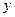Можно предположить, что возрастает по , т.е. репрезентативный агент получает более высокую полезность в случае высокого агрегированного выпуска. Например, в модели из раздела 6.4 увеличение агрегированного выпуска сдвигает вправо кривую спроса на продукцию репрезентативной фирмы. Это приводит к увеличению реальной цены, которую фирма может получить для данного собственного объема производства. 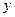Если же возрастает по , то равновесие с более высоким объемом агрегированного выпуска будет соответствовать более высокому уровню благосостояния. Действительно, рассмотрим два равновесных объема выпуска и , так что . Т.к. 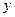возрастает по , то 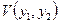будет выше, чем . И с учетом того, что - это равновесие, а значит, максимизирует для данного 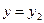, мы получаем, что 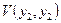превосходит по величине 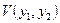. Так что репрезентативный агент извлекает большую полезность в состоянии равновесия с более высоким выпуском.[40]

Модели с множеством равновесий, ранжируемых по Парето, относятся к классу моделей с провалами координации. Возможность нескоординированности приводит к тому, что экономика может застрять в равновесии с недозанятостью ресурсов. При этом выпуск может оказаться неэффективно низким только потому, что все верят, что именно так и случится. Проблема состоит в том, что в данной ситуации не существует сил, способных вернуть выпуск к нормальному уровню. В результате, может потребоваться определенная политика государства, направленная на координацию ожиданий с целью перехода в равновесие с высоким выпуском. Так, например, временное стимулирование может перевести экономику в лучшее равновесие на постоянной основе.

Между проблемой множества равновесий и проблемой реальной жесткости, которую мы обсуждали выше, существует важная взаимосвязь. Вспомним, что мы подразумевали под высокой степенью реальной жесткости такую ситуацию, когда в ответ на увеличение уровня цен и последующее падение агрегированного выпуска репрезентативная фирма желает менять свою относительную цену лишь незначительно. С точки зрения выпуска, это соответствует функции реакции с наклоном несколько меньшим 1: когда агрегированный выпуск падает, репрезентативная фирма готова снизить свой объем производства почти так же, как и остальные. Если существует множество равновесий, снижение агрегированного выпуска в определенном диапазоне должно заставлять репрезентативную фирму увеличивать свою цену и снижать объем производства относительно других фирм. Другими словами, необходимо, чтобы на определенном интервале функция реакции фирмы имела наклон больше 1. Т.е., нескоординированность требует существования на определенном интервале высокой степени реальной жесткости.

Следовательно, т.к. существует много потенциальных источников реальной жесткости, то существует и много потенциальных источников нескоординированности. Многие модели подходят под общую логику, предлагаемую Купером и Джоном. Примерами таких работ являются Diamond (1982), Bryant (1983), Shleifer (1986), Kiyotaki (1988), Howitt and McAfee (1988), Murphy, Shleifer, and Vishny (1989), Pagano (1989), Matsuyama (1991), Durlauf (1993), Gali (1994) и Lamont (1995).

Дата добавления: 2015-10-30