Эмпирическое приложение: экспериментальный анализ нескоординированности

Модели с провалами координации характеризуются множеством равновесий по Нэшу. Традиционная теория игр говорит о том, что экономика окажется в одном из равновесий, но она не может предсказать в каком конкретно. Различные теории уточняющего выбора равновесий делают предсказания относительно того, какое равновесие может установиться. Например, традиционная точка зрения заключается в том, что Парето-доминирующее равновесие будет являться фокальной точкой, и что экономики, находящиеся в ситуации потенциальной нескоординированности, тем не менее, приходят в лучшее из возможных равновесий. Существуют и другие возможные объяснения. Например, может быть так, что каждый агент не уверен в том, какому правилу следуют другие агенты для выбора возможного исхода, и в результате в таких экономиках ситуация равновесия оказывается недостижимой.

Один из широко распространенных в последние годы подходов к тестированию теорий - это использование экспериментов. Преимущество экспериментов заключается в том, что они позволяют исследователям точно контролировать экономическую среду. Основным недостатком экспериментов является то, что они очень часто оказывается невыполнимыми и поведение в лабораторных условиях и на практике в одинаковых ситуациях может сильно отличаться.

Van Huyck, Battalio, and Beil (1990, 1991) и Cooper, DeJong, Forstyhe, and Ross (1990, 1992) тестировали теории провалов координации с помощью экспериментов. Van Huyck, Battalio, and Beil (1990) рассматривали координационную игру, предложенную в работе Bryant (1983). В игре Брианта каждый из 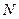агентов выбирает уровень усилий из интервала . Выигрыш 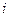-го агента имеет вид:

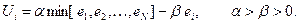(6.97)

Ситуация, когда все агенты выбирают максимальный уровень усилий 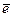, дающий им выигрыш в размере 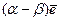, является наилучшим равновесием. Но также любой одинаковый для всех агентов уровень усилий из интервала является равновесием по Нэшу: если каждый агент, за исключением агента 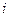, выбирает уровень усилий 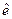, то 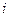-ый агент также предпочтет выбрать уровень усилий 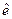. Т.к. в случае, когда все агенты выбирают одинаковый уровень усилий, их выигрыши возрастают по сравнению с обратной ситуацией, то игра Брианта – это модель провала координации с континуумом равновесий.

Ван Хук, Батталио и Бейл рассматривали версию игры Брианта, в которой усилия могли принимать только целочисленные значения от 1 до 7, 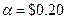, , и 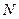лежало между 14 и 16[41]. Они сделали несколько основных выводов. Первый вывод касается ситуации, когда группа играет в игру первый раз. Т.к. модель игры Брианта не является повторяющейся, то эта ситуации наиболее близка к результатам модели. Ван Хук, Батталио и Бейл выявили, что в первой игре равновесие не достигается вовсе. Наиболее часто выбираемые уровни усилий – это 5 и 7, но дисперсия при этом очень высокая. Следовательно, никакая детерминистическая теория выбора единственного равновесия не может успешно описать поведение.

Во-вторых, повторяющийся характер игры обуславливает стремительное движение в сторону наименьшего уровня усилий. В пяти из семи экспериментальных групп минимальный уровень усилий в первом периоде был строго больше 1. Но к четвертому периоду игры во всех семи группах минимальный уровень усилий достигал 1 и оставался на этом уровне во всех последующих периодах. Таким образом, степень нескоординированности является высокой.

В-третьих, игра не сходится ни к одному равновесию. Каждая группа участвовала в игре 10 раз, в общей сложности – 70 испытаний. Ни в одном из 70 испытаний все игроки не выбрали одинаковый уровень усилий. Даже в последних 7 испытаниях, которые следовали уже после того, как во всех группах наступила череда испытаний, в которых минимальный уровень усилий составлял 1, больше четверти игроков выбирали уровень усилий выше 1.

И, наконец, даже изменение функции выигрышей с целью достижения «скоординированности» не предотвращает возвращения к неэффективным исходам. После начальных 10 испытаний, каждая группа прошла еще через пять испытаний с параметром 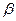из (6.97), равным 0. При 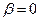издержки увеличения усилий отсутствуют. В результате, большинство групп (хотя и не все) стали приближаться к Парето-эффективному равновесию, где уровень усилий равен 7 для всех игроков. Но когда 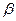вновь снизили до , произошел стремительный возврат к ситуации, когда большинство игроков выбирало минимальный уровень усилий.

Результаты, полученные Ван Хуком, Батталио и Бейлом, говорят о том, что предсказания дедуктивных теорий поведения должны трактоваться с осторожностью: несмотря на то, что игра Брианта весьма простая, реальное поведение агентов на практике далеко не во всем соответствует предсказаниям любой стандартной теории. Результаты также показывают, что в моделях провалов координации может возникнуть сложная экономическая динамика.

Дата добавления: 2015-10-30