Практична частина. Для виконання практичної частини лабораторної роботи необхідно:

Для виконання практичної частини лабораторної роботи необхідно:

1. Скласти таблицю відомих параметрів задачі.

2. Вводячи відповідні позначення, вказати можливі стани природи та їх ймовірності.

3. З огляду на економічний зміст задачі, скласти матрицю виграшів (рис.15).

4. Використовуючи дані платіжної матриці, скласти матрицю ризиків.

5. Проаналізувавши матрицю ризиків, відзначити в ній стратегії, які є явно програшними (для яких всі значення ризику перевищують відповідні значення іншої стратегії).

Платіжна матриця (таблиця виграшів)
	П1	П2	П3	П4	П5
А1
А2				-150	-300
А3				-50	-250
А4					-100
А5
А6					-50
Максимум

Рис.15.

6. На основі утворених матриць скласти таблицю показників для різних критеріїв (5.10)-(5.13). Для критерію Гурвіца розглянути випадки значень параметру песимізму 0; 0,2; 0,4; 0,6; 0,8.

7. Враховуючи розраховані критеріальні показники, вказати рекомендовану оптимальну стратегію гравця.

Лабораторна робота №6:«Оцінювання ступеня ризику

неповернення кредиту»

Ntilde; Ключові слова: кореляційна модель, модель Чессера, модель Альтмана, коваріаційна матриця, дискримінантна функція.

s Контрольні запитання:

1. Сформулюйте зміст задач статистичного аналізу.

2. В чому полягає алгоритм побудови дискримінантної моделі?

Теоретична частина

Ймовірність настання певної несприятливої події в кредитуванні, яка є визначальною мірою кредитного ризику і застосовується у розрахунку більшості його кількісних показників, може бути визначена об'єктивним або суб'єктивним способом.

Об'єктивний спосіб визначення кредитного ризику базується на застосуванні різноманітних статистичних методів. Одним з розділів статистичної науки є факторний статистичний аналіз, який розв'язує класифікаційні задачі – розбиття визначеної сукупності об'єктів на класи шляхом побудови так званої класифікуючої функції у вигляді кореляційної моделі.

Однією з найвідоміших кореляційних моделей на Заході є модель нагляду за кредитами Чессера і Z-модель Альтмана (модель прогнозування банкрутства). Однак, обидві моделі відповідають умовам розвинутої ринкової економіки. Для умов України розроблені адекватні моделі, які дозволяють розділити позичальників з простроченою заборгованістю за кредитами і позичальників, у яких такої заборгованості немає. Розроблені моделі включають такі показники:

1) коефіцієнт покриття К_п, тобто відношення поточних активів до короткострокових зобов'язань;

2) коефіцієнт фінансової залежності К_фз як відношення позичених коштів до загальної вартості активів.

Алгоритм знаходження цієї моделі є таким. Розглядають дві сукупності позичальників – Х (без простроченої заборгованості) і Y (з простроченою заборгованістю):

; ,

де n₁ – кількість позивальників сукупності Х; n₂ – кількість позичальників сукупності Y; x_1j, y_1l – коефіцієнти покриття (К_п); x_2j, _y2l – коефіцієнти фінансової залежності (К_фз); j = 1, …, n₁; l = 1, …, n₂.

1. Для матриць вхідних даних Х та Y визначають оцінки векторів середніх значень х_с і у_с та коваріаційних матриць S_x i S_y:

, ,

, ,

де ; ; ; .

2. Розраховують незміщену оцінку сумарної коваріаційної матриці:

.

3. Обчислюють обернену матрицю .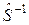

4. Обчислюють вектор оцінки коефіцієнтів дискримінантної функції:

.

5. Знаходять оцінки дискримінантної функції:

,

де X^T і Y^T – матриці, транспоновані до матриць X і Y.

6. Обчислюють середні значення

.

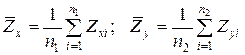7. Знаходять межу дискримінації:

.

8. Записують дискримінантну функцію (модель):

.

Якщо Z ³ C, то позичальника слід віднести до сукупності Х, а якщо Z £ C, то до сукупності Y.

Дата добавления: 2015-10-29