Теоретична частина. Симплексний метод є основним методом при розв’язуванні задач лінійного

Симплексний метод є основним методом при розв’язуванні задач лінійного програмування (ЛП). Для використання цього методу задача ЛП повинна бути записана у канонічній формі:

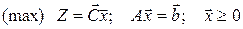, (2.1)

де А – матриця умов задачі розміром m ´ n, ранг якої рівний m.

Частковим випадком канонічної задачі (2.1) є так звана задача в базисній формі, в якій коефіцієнти вектора обмежень невід’ємні і у кожному рівнянні є змінна з коефіцієнтом 1, яка не входить до жодного з решти рівнянь системи обмежень. Змінна з такими характеристиками називається базисною.

Найзручнішим методом приведення системи обмежень до базисного вигляду є метод виключень Жордана-Гаусса. Він дозволяє розв’язати систему шляхом перетворення її в еквівалентну систему з одиничним базисом або встановити її несумісність. На кожному кроці одна із змінних стає базисною: виключається з усіх рівнянь, крім одного, де залишається з коефіцієнтом 1.

Розглянемо детальніше один з кроків жорданових перетворень. Нехай змінна х_s входить у рівняння r з коефіцієнтом а _rs ¹ 0. Для того, щоб зробити її базисною, розділимо дане рівняння на а _rs і результат віднімемо від кожного рівняння системи крім рівняння r, домножуючи його кожний раз на відповідний коефіцієнт а _is (отримуючи при цьому змінну x_s з коефіцієнтом 0).

Формули, за якими будуть проводитись розрахунки коефіцієнтів нової системи, отриманої в результаті одного кроку жорданових перетворень з ключовим елементом а _rs, мають вигляд:

(2.2)

(2.3)

Обчислення за наведеними формулами (2.2)-(2.3) можна описати при допомозі так званого «правила прямокутника»: щоб знайти перетворений елемент матриці А, потрібно від елемента відняти добуток коефіцієнтів, що стоять навпроти нього у ключових рядку і стовпчику, поділений на ключовий елемент, розташований по діагоналі від елемента (рис.3).

Рис.3.

Алгоритм симплекс-методу складається з таких етапів:

Ø Переглядають знаки всіх коефіцієнтів D_і оціночного рядка симплексної таблиці. Якщо всі D_і ³ 0, то задача розв’язана: даний допустимий розв’язок є оптимальним. Якщо в оціночному рядку є від’ємні коефіцієнти, переходять до наступного пункту.

Ø Серед значень D_і < 0 знаходять найбільше за абсолютною величиною і відповідний стовпчик вважають ключовим (наприклад, стовпчик s). Якщо у ключовому стовпчику всі елементи a_is £ 0, то цільова функція необмежена, і Z_max = ¥, тобто розв’язування задачі припиняють. Якщо не всі a_is £ 0, переходять до наступного кроку.

Ø Для кожного додатнього елемента ключового стовпчика знаходять симплексне відношення b_i / a_is, вибирають рядок з найменшим значенням і його вважають ключовим рядком. Елемент на перетині ключового рядка і ключового стовпчика буде ключовим елементом.

Ø Виконують жорданове перетворення за наведеними вище формулами, після чого переходять до першого пункту алгоритму.

При переході від однієї симплекс-таблиці до іншої доцільно здійснювати контроль обчислень. Для цього кожного разу обчислюють елементи контрольного стовпчика за правилом прямокутника, а потім додаванням елементів рядка нової таблиці перевіряють отриманий результат. Вони повинні співпасти.

Дата добавления: 2015-10-29