Теоретична частина. Класична транспортна задача (ТЗ) або транспортна задача в матричній постановці

Класична транспортна задача (ТЗ) або транспортна задача в матричній постановці формулюється так.

Є в наявності m пунктів виробництва певної однорідної продукції та n пунктів її споживання. Відомі запаси а _і (і = 1,..., m) продукції в кожному пункті-виробнику (назвемо їх постачальниками), попит b_j (j = 1,..., n) кожного пункту-споживача та витрати C_ij на перевезення одиниці продукції від кожного постачальника до кожного споживача. Припускається, що сумарні запаси постачальників дорівнюють сумарному попитові споживачів, і a_i > 0, b_j > 0, C_ij ³ 0 для всіх і = 1,..., m та j = 1,..., n. Необхідно скласти план перевезень продукції (план закріплення постачальників за споживачами) з мінімальними затратами, при якому повністю вивезена від постачальників продукція задовольнила б загальний попит споживачів.

У математичних позначеннях транспортна задача виглядає як задача мінімізації цільової функції

при виконанні умов

та

,

де x_ij – об’єм перевезень від постачальника i до споживача j.

Це типова задача лінійного програмування у канонічному вигляді з числом змінних (m ´ n) і числом рівнянь-обмежень (m + n). Тому вона може бути розв’язана за допомогою симплекс-таблиць. Однак, у випадку транспортної задачі ці таблиці дещо модифіковані й називаються таблицями перевезень.

Найпоширенішими методами побудови початкового опорного плану ТЗ є діагональний метод (метод північно-західного кута), метод найменшої вартості та метод усереднених коефіцієнтів. Різниця між ними полягає у порядку заповнення таблиці перевезень.

Для діагонального методу характерне заповнення, починаючи з лівого верхнього, «північно-західного» кута (клітинки) таблиці з поступовим вичерпанням запасів постачальників та задоволенням потреб споживачів.

При використанні методу найменшої вартості заповнення проводять за принципом зростаючої питомої вартості перевезень з виконанням тих самих умов.

Метод усереднених коефіцієнтів вимагає попереднього розрахунку середніх вартостей кожного рядка і стовпчика:

;

,

а потім обчислення усереднених коефіцієнтів за виразом

,

після чого заповнюють клітинки таблиці перевезень у порядку зростання усереднених коефіцієнтів K_ij.

Наведені методи створення опорного плану ТЗ не дають відповіді на основне питання задачі – питання оптимальності отриманого плану перевезень. Для отримання такої відповіді застосовують метод потенціалів. Алгоритм методу потенціалів полягає в наступному:

v Кожному рядкові та стовпчикові надають деякі числа (потенціали) a_і та b_j, для яких має виконуватися рівність стосовно клітинок, заповнених одним з перерахованих вище методів створення початкового опорного плану. Оскільки заповнених клітинок (m + n – 1), а потенціалів має бути (m + n), то значення одного з потенціалів вибирають довільно, наприклад, 0.

v Для порожніх клітинок таблиці перевезень перевіряють співвідношення між величиною C_ij та сумою відповідних потенціалів. Якщо для всіх незаповнених клітинок виконується умова , значить, даний опорний план перевезень є оптимальним, і задачу вважають розв’язаною.

v Якщо в таблиці є клітинки, для яких , то, починаючи з клітинки з найбільшою різницею, будують цикл перевезень. При побудові циклу виходять із вказаної клітинки і повертаються до неї по ламаній лінії, причому повороти можна робити лише в заповнених клітинках. Для уникнення порушення балансу перевезень в таблиці при циклових перетвореннях у клітинках повороту почергово додають і віднімають k одиниць до (від) наявних у них об’ємів перевезень (рис.10). Величина k визначається найменшим з обсягів перевезень у клітинках таблиці, де відбувається віднімання.

Рис.10.

Оскільки цикл міститиме парну кількість кутів, то у половині кутів величина k додається, а у половині – віднімається, тобто баланс не порушиться.

v Після перерахунку перевезень по циклу повертаються до першого пункту алгоритму і так роблять до тих пір, доки для всіх порожніх клітинок не виконуватиметься умова .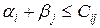

Отриманий план перевезень буде оптимальним, оскільки йому буде відповідати мінімальна сумарна вартість перевезень.

Якщо розглянути суть потенціалів як параметрів транспортної задачі, то, враховуючи систему умов існування оптимального розв'язку, нескладно побачити, що потенціали – це оцінки задачі, двоїстої до транспортної.

Дата добавления: 2015-10-29