Теоретична частина. Графічний метод розв'язування оптимізаційних задач дозволяє максимально

Графічний метод розв'язування оптимізаційних задач дозволяє максимально візуалізувати процес знаходження розв'язку. Кожна нерівність системи лінійних нерівностей (обмежень) виду

(1.1)

геометрично визначає на площині х₁Ох₂ півплощину з граничною прямою 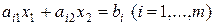. Умови не-від’ємності визначають півплощини відповідно з граничними прямими х₁ = 0 та х₂ = 0. Система (1.1) сумісна, тому півплощини, як опуклі множини, перетинаючись, утворюють спільну частину, яка є опуклою множиною і сукупністю точок, координати кожної з яких є розв’язком даної системи.

Сукупність цих точок (розв’язків) називається многокутником розв’язків. У загальному випадку він може бути (залежно від розмірності простору) точкою, відрізком, променем, многокутником або необмеженою багатокутною областю. Якщо в задачі кількість змінних n більша від 2, то говорять про многогранник розв’язків.

Геометрична інтерпретація задачі лінійного програмування полягає в пошуку такої точки многогранника розв’язків, координати якої надають лінійній функції екстремального значення. Допустимими розв’язками є всі точки многогранника.

Обмежимось випадком n = 2. Оскільки, згідно теореми, оптимальне значення розв’язку задачі лінійного програмування досягається у вершині многокутника розв’язків, то зміст такої задачі з геометричної точки зору можна представити як знаходження у многокутнику розв’язків такої вершини, де цільова функція 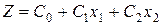набуває найбільшого (або найменшого) значення.

Геометрична інтерпретація задачі лінійного програмування дозволила створити графічний метод її розв’язування, основними складовими якого є такі пункти:

1. Побудова многокутника розв’язків, як перетину окремих півплощин розв’язків, утворених нерівностями системи.

2. Відшукання оптимальної точки. Для її визначення використовують вектор нормалі прямої , який є вектор-градієнтом функції Z і вказує напрям її зростання. Лінія, перпендикулярна до вектора нормалі, називається лінією рівня і аналітично записується так:

.

Пересуваючи лінію рівня перпендикулярно до 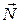у напрямку вектора нормалі, можна знайти вершину, де функція Z(x) набуває найбільшого значення. Для відшукання точки мінімуму Z(x) треба зсувати лінію рівня в протилежному до 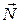напрямку. Тобто, вектор 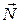дозволяє на одному графіку одночасно знайти максимум і мінімум цільової функції – розв’язати дві екстремальні задачі при одній і тій же системі обмежень.

3. Обчислення оптимальних значень. Для цього знаходять координати вершин мінімуму і (або) максимуму як спільний розв’язок рівнянь відповідних граничних прямих, що перетинаються у оптимальних вершинах многокутника розв’язків. Знайдені координати підставляють у рівняння цільової функції й обчислюють Z_min i Z_max.

Дата добавления: 2015-10-29