Теоретична частина. У багатьох задачах доводиться оцінювати наслідки прийняття того чи іншого рішення в

У багатьох задачах доводиться оцінювати наслідки прийняття того чи іншого рішення в умовах невизначеності. Суть цієї невизначеності може мати різну природу. Розглядатимемо лише ті випадки невизначеності, коли вона зумовлена усвідомленою поведінкою кількох учасників операції. Ці учасники (гравці), як правило, переслідують різні цілі, причому результат будь-якого рішення кожного з них залежить від рішень, прийнятих іншими учасниками. Ситуації такого роду називають конфліктними.

Нехай гравець А має в своєму розпорядженні m альтернативних рішень, а гравець В має n рішень, тобто 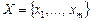і – множини можливих рішень гравців А і В відповідно. Пару (х, у) прийнятих рішень називають бістратегією або наслідком гри.

Припустимо, що значення F_ij º F(x, y) виграшу гравця А (програшу гравця В) для кожної бістратегії (x_і, y_j) відоме. Всі значення { F_ij } можна записати у вигляді матриці, рядки якої відповідають стратегіям { x_i } гравця А, а стовпчики – стратегіям { y_j } гравця В. Таку матрицю називають платіжною матрицею або матрицею гри.

Нехай гравець А вибирає стратегію х_і; тоді в найгіршому випадку він отримає виграш min (F_ij). Передбачаючи таку можливість, гравець А повинен вибрати таку стратегію, щоб максимізувати свій мінімальний виграш a:

. (5.1)

Величина a – гарантований виграш гравця А – називається нижньою ціною гри. Стратегія х_і0, яка забезпечує отримання a, називається максимінною стратегією.

Гравець В, вибираючи стратегію, виходить з того принципу, що при виборі деякої стратегії y_j його програш не перевищить максимального зі значень елементів j -того стовпчика матриці, тобто буде меншим або дорівнюватиме mах (F_ij). Розглядаючи множину mах (F_ij) для різних j, гравець В, звичайно, вибере таке значення j, при якому його максимальний програш b мінімізується:

. (5.2)

Величина b називається верхньою ціною гри, а відповідна стратегія y_j0 – мінімаксною.

Фактичний виграш гравця А при розумних діях партнерів обмежений нижньою і верхньою ціною гри. Якщо ж ці вирази рівні, тобто

, (5.3)

то такий варіант називається грою з сідловою точкою. В матриці гри з сідловою точкою завжди існує елемент, який є одночасно мінімальним у своєму рядку і максимальним у своєму стовпчику; такий елемент і називають сідловою точкою.

Сідловій точці відповідає пара мінімаксних рішень; ці рішення називають оптимальними, а їх сукупність – розв’язком гри або оптимальною стратегією.

Розв’язок гри має таку властивість: якщо один з гравців дотримується свого оптимального рішення, то іншому не вигідно відхилятися від свого оптимального рішення.

З означення сідлової точки зрозуміло, що якщо платіжна матриця не містить сідлової точки, то для таких ігор a < b. Виграш гравців не перевищуватиме b, а програш буде не меншим від a. Пошук рішення в цьому випадку заставить гравців впродовж гри застосувати не одну, а кілька стратегій, вибір яких буде здійснюватись випадковим чином, залежно від поведінки суперника. Такий випадковий вибір гравцем своїх стратегій називається змішаною стратегією.

Очевидно, що результат гри при застосуванні гравцями змішаних стратегій має стохастичний характер, оскільки вибір гравцями своїх стратегій пов’язаний з певною ймовірністю. Змішані стратегії є математичною моделлю гнучкої тактики, дотримання якої робить практично неможливим для суперника отримання інформації про прийняте рішення.

В теорії ігор є важлива теорема – теорема про оптимальну змішану стратегію, яка формулюється так: якщо один із гравців застосовує змішану оптимальну стратегію, то його виграш дорівнює ціні гри g незалежно від того, з якими частотами другий гравець буде застосовувати свої стратегії, що увійшли в оптимальну.

Використання теореми про оптимальну змішану стратегію дає можливість привести задачу пошуку оптимальних змішаних стратегій до задачі лінійного програмування.

Розглянемо гру, матриця якої має розмірність m ´ n:

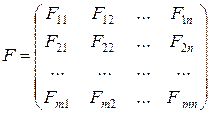. (5.4)

Матриця (за умовою) не має сідлової точки, тому розв’язок гри буде представлений змішаними стратегіями і .

При оптимальній стратегії гравця А має виконуватися умова

, (5.5)

а при оптимальній стратегії гравця В – умова

. (5.6)

Отже, можна розглядати задачу пошуку оптимальної стратегії гравця А, для якої мають місце обмеження

(5.7)

Ціна гри невідома, однак можна вважати, що g > 0. Розділимо всі доданки нерівностей системи (5.7) на g. Отримаємо нову систему:

(5.8)

де .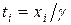

Оскільки (з точки зору гравця А) розв’язок гри має максимізувати значення g, то функція має набути мінімального значення. Тобто, ми отримали задачу лінійного програмування: мінімізувати цільову функцію при виконанні обмежень (5.8) і умов не-від’ємності змінних t_i.

Розв’язуючи сформульовану задачу, знаходимо t_i і величину 1/ g, звідки можна отримати х_і = gt_i.

В окремих ситуаціях невизначеність пов'язана не з діями конкретного учасника гри, а зі станом навколишнього середовища. Такі конфліктні ситуації називаються іграми з природою. Природу розглядають не як зацікавлену сторону, а як інстанцію з невідомою поведінкою, що свідомо не протидіє планам гравця.

На відміну від «звичайних» ігор поведінку природи описують не стратегіями, а станами П, кількість і опис яких визначає сам гравець. Така задача є складнішою, оскільки не існує критерію вибору поведінки природи. Тому вводять показник ризику, що описує «вдалість» застосування гравцем А тієї чи іншої стратегії з урахуванням стану природи.

Ризиком r_ij при стратегії А_і в умовах П_j називають різницю між прогнозованим оптимальним виграшем і виграшем, який отримується насправді:

, (5.9)

де , тобто виграш гравця А в оптимальному варіанті. Отримані значення ризиків записують у вигляді матриці, аналогічної до матриці виграшів.

З огляду на відсутність у діях природи «розрахунку» для вибору кращої стратегії розроблено цілий ряд спеціальних критеріїв, основними з яких є:

1) критерій Байєса-Лапласа, який ґрунтується на припущенні про відомі ймовірності станів природи, і згідно з яким оптимальною вибирають ту зі стратегій гравця А, для якої середнє значення чи математичне сподівання виграшу перетворюється на максимум:

, (5.10)

причому обов'язковим є виконання умови (враховані всі можливі стани природи);

2) максимінний критерій Вальда («критерій крайнього песимізму»), згідно з яким найкращим рішенням буде те, для якого виграш виявиться максимальним з усіх мінімальних, при різних варіантах умов:

; (5.11)

3) мінімаксний критерій Севіджа («критерій мінімального ризику»), за яким оптимальним оголошується не максимальний виграш, а мінімальний ризик; тому працює критерій з матрицею ризиків:

. (5.12)

4) критерій Гурвіца («критерій песимізму-оптимізму»), який рекомендує в умовах невизначеності вибрати щось усереднене між крайнім песимізмом і крайнім оптимізмом:

, (5.13)

де 0 < c < 1 – коефіцієнт («параметр песимізму»), який вибирається з суб’єктивних міркувань: чим небезпечніша ситуація, тим ближче до одиниці вибирають значення коефіцієнта. Як правило, менеджери встановлюють значення коефіцієнта c залежно від ступня впевненості у правильності свого вибору (якому з варіантів слід віддати перевагу)[ii].

---

Дата добавления: 2015-10-29