Теоретична частина. У багатьох задачах, пов'язаних з обробкою статистичної інформації

У багатьох задачах, пов'язаних з обробкою статистичної інформації, виникає необхідність визначення вигляду залежності між двома величинами зі статистичним характером самої залежності. Однією з найпростіших методик у таких ситуаціях є метод найменших квадратів (МНК), що належить до регресійних методів оцінювання параметрів.

Маючи дві залежні випадкові величини Х та Y, представимо одну з них як функцію іншої. Допустимо, що деякі підстави дозволяють нам обмежитись наближеним представленням (оскільки в даному випадку точне наближення неможливе!) величини Y у вигляді лінійної функції від Х (тобто, сама залежність є квазілінійною):

(4.1)

або

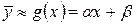, (4.2)

де a і b – параметри, які необхідно підібрати так, щоб за допомогою залежності g(x) найкраще узгодити дані емпіричних спостережень зі значеннями, отриманими з виразу 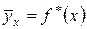[i].

Нехай вивчається система кількісних ознак (Х, Y). В результаті n незалежних випробувань отримали n пар чисел (х₁, у₁), (х₂, у₂), …, (х_n, у_n). Знайдемо вигляд вибіркового рівняння прямої лінії середньоквадратичної регресії. Оскільки різні значення х^* ознаки Х і відповідні до них значення у^* ознаки Y спостерігали по одному разу, – немає необхідності їх групувати і знаходити середнє. Тому загальний вигляд шуканого рівняння можна представити так:

.

Кутовий коефіцієнт прямої лінії Y по Х називають вибірковим коефіцієнтом регресії Y по Х і позначають b; він є оцінкою коефіцієнта регресії b.

Підбираючи параметри b та k так, щоб сума квадратів відхилень була мінімальною (для цього прирівнюють до нуля відповідні частинні похідні), отримують вирази:

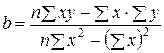, (4.3)

. (4.4)

Якщо графік регресії не є прямою лінією, то регресію називають нелінійною або криволінійною. Для визначення вигляду функції регресії будують точки (х, ) й за їх розташуванням роблять висновок про приблизний вигляд функції регресії. Для остаточного висновку необхідно враховувати особливості конкретної економічної задачі, що розв’язується.

Для перевірки побудованої теоретичної моделі процесу на адекватність (відповідність реальності) застосовують коефіцієнт кореляції

, (4.5)

де величина у чисельнику називається кореляційним моментом.

Для дискретних випадкових величин кореляційний момент розраховується за формулою

, (4.6)

а для неперервних –

. (4.7)

Коефіцієнт кореляції r_ху задовольняє умову (–1 £ r_ху £ 1) і визначає ступінь лінійної ймовірнісної залежності між випадковими величинами.

Дві випадкові величини, для яких коефіцієнт кореляції дорівнює нулю, називають некорельованими. У протилежному випадку ці величини називаються корельованими. При | r_ху | = 1 випадкові величини пов’язані між собою лінійною залежністю.

Зауважимо, що незалежні випадкові величини завжди некорельовані, тобто для них завжди виконується рівність . Однак, зворотне твердження є некоректним. Рівність нулю коефіцієнта кореляції не завжди означає незалежність випадкових величин, оскільки залежні випадкові величини можуть бути як корельованими, так і некорельованими.

При дослідженні нелінійних залежностей теж використовують МНК. Наприклад, для розрахунку параметрів квадратичної залежності 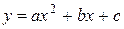можна використати формули:

; ; , (4.8)

якщо виконується умова 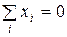. Якщо ж така умова не виконується, то відповідні параметри квадратичної залежності можна знайти, розв’язавши систему рівнянь

(4.9)

одним з відомих методів (Крамера, Гаусса та ін.)

Дата добавления: 2015-10-29