Теоретична частина. Задачі розвитку і розташування виробництва характеризуються значною розмірністю

Задачі розвитку і розташування виробництва характеризуються значною розмірністю, зумовленою високим ступенем деталізації задач такого роду. Ця специфіка не дозволяє отримувати універсальні моделі, які можна було б застосовувати для різних галузей виробництва одночасно. Однак, важливим моментом дослідження таких задач є методи їх розв'язування, придатні для всіх задач поточного виробничого планування в межах певного об'єднання. Значна деталізація, з одного боку, дійсно призводить до збільшення розмірності моделі, та з іншого одночасно дозволяє отримати специфічний вигляд матриці задачі.

Нехай розглядається об'єднання підприємств, при побудові моделі функціонування якого використані такі позначення:

k – індекс підприємства, що входить до об'єднання (k = 1, 2, …, K);

j_k – індекс виду продукції, що виробляється на k -тому підприємстві (j_k = 1, 2, …, n_k);

i_k – індекс «власного» ресурсу підприємства k (i_k = 1, 2, …, m_k);

i – індекс виду ресурсу, загального для підприємств об'єднання (i = 1, 2, …, m);

X_k – вектор випуску продукції k -тим підприємством (розмірністю n_k × 1);

B_k – вектор запасів локальних ресурсів i_k, що споживаються k -тим підприємством (розмірністю m_k × 1);

– вектор запасів загальних ресурсів і (розмірністю m × 1);

М_k – вектор питомого прибутку від випуску продукції k-тим підприємством (розмірністю 1 × n_k);

A_k – матриця коефіцієнтів (норм) затрат локальних ресурсів на випуск продукції k -тим підприємством (розмірністю m_k × n_k);

– матриця коефіцієнтів (норм) затрат загальних ресурсів на випуск продукції k -тим підприємством (розмірністю m × n_k);

Використання уведених позначень дозволяє скласти математичну модель об'єднання в такому вигляді:

(10.1)

(10.2)

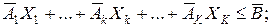(10.3)

(10.4)

Структура задачі поточного планування на рівні об'єднання дає змогу розділення її на окремі під-задачі зі значно меншою розмірністю та їх взаємопов'язане розв'язування в рамках ітеративного процесу. Для знаходження остаточного розв'язку можна застосувати різні методи. Розглянемо деякі з них.

Метод розкладання Данціґа-Вулфа. Метод передбачає розкладання вихідної задачі (10.1)-(10.4) на локальні задачі окремих частин об'єднання (підприємств) і головну задачу (об'єднання в цілому), пов'язуючи ці задачі.

Модель головної задачі виглядає так:

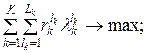(10.5)

(10.6)

(10.7)

(10.8)

. (10.9)

де l_k – індекс (номер) базисного плану k -того підприємства (l_k = 1, 2, …, L_k); – вектор випуску продукції k -того підприємства за базисним планом l_k (розмірністю n_k × 1);

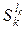– вектор витрати загальних ресурсів на весь випуск (розмірністю m × 1):

; (10.10)

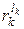– увесь обсяг прибутку від випуску :

; (10.11)

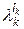– питома вага (вклад), з якою базисний план l_k підприємства k увійде до плану об'єднання в головній задачі. Тобто, будь-який допустимий план X_k підприємства в задачі об'єднання є лінійною комбінацією (10.9).

Головна задача (10.5)-(10.9) еквівалентна до вихідної задачі (10.1)-(10.4). Слід відзначити, що розмірність головної задачі суттєво менша за розмірність вихідної, оскільки для кожного підприємства вказаний не цілий блок обмежень вигляду (10.2), а всього одне обмеження вигляду (10.7), яке описує підприємство гранично агреговано.

Метод дворівневого планування Корнаі-Ліптака. В даному методі ітераційний процес оптимізації планів розвитку об'єднання в цілому і підприємств зокрема базується не на коригуванні двоїстих оцінок ресурсів і продукції, а на коректуванні запасів ресурсів для підприємств і завдань з випуску продукції у натуральному вираженні згідно з аналізом і порівнянням граничних ефективностей їх використання на підприємствах.

Нехай вихідна задача має той самий вигляд (10.1)-(10.4). Увівши поділ векторів запасів загальних ресурсів за підприємствами

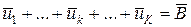, (10.12)

де 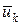– вектор запасів загальних ресурсів, виділених k -тому підприємству, отримаємо такий вигляд задачі:

(10.13)

(10.14)

(10.15)

(10.16)

Задача (10.13)-(10.16) автоматично розпадається на секторні задачі, які для кожного k -того підприємства матимуть такий вигляд:

(10.17)

(10.18)

(10.19)

(10.20)

Дата добавления: 2015-10-29