
Читайте также:
|
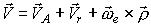
Дифференцируя это выражение по времени получаем,
 (11)
(11)
В выражении (11) V' = aA является ускорением начала подвижной системы координат; ωe = εe является угловым ускорением переносного движения или угловым ускорением вращения подвижной системы координат в неподвижной. Векторы Vr и ρ известны в проекциях на оси подвижной системы координат и изменяются по величине и направлению, поэтому, согласно теореме об абсолютной производной вектора,
 (12)
(12)
В выражениях (12) локальная производная вектора скорости характеризует быстроту его изменения в подвижной системе координат и является относительным ускорением. Таким образом, из (11) имеем
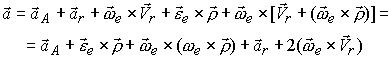 (13)
(13)
Для выделения переносного ускорения используем прием останова, принимая в (13) ar = 0 и Vr = 0. Когда точка остановлена в подвижной системе координат (вморожена в подвижную систему координат), она за счет движения подвижной системы координат переносится относительно неподвижной, и ее абсолютное ускорение равно переносному ускорению a = ae. Учитывая это, из (13) получаем
 (14)
(14)
то есть переносное ускорение совпадает с ускорением той точки подвижной системы координат, где в данное мгновение времени находится материальная точка, если принять подвижную систему координат за твердое тело. Картина движения будет нагляднее, если подвижный трехгранник Ox1y1z1 на рис. 105 принять за ледяной трехгранник, где в данный момент времени, в данном положении вморожена точка M.
Подставляя выражение (14) в (13), имеем
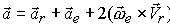 (15)
(15)
Последнее слагаемое в (15) называется кориолисовым ускорением и обозначается ac. Таким образом, имеем математическую запись теоремы:
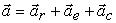 (16)
(16)
которую можно сформулировать так: абсолютное ускорение точки, участвующей в сложном движении, равно геометрической сумме относительного, переносного и кориолисова ускорений.
Остановимся на кориолисовом ускорении, равном
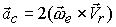 (17)
(17)
Величина кориолисова ускорения вычисляется по формуле
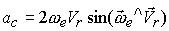 (18)
(18)
а направление вектора определяется по правилу построения вектора векторного произведения векторов ωe и Vr (рис. 106, a). Когда переносное и относительное движение лежат в одной плоскости, построение вектора кориолисова ускорения облегчается применением правила Н.Е. Жуковского. В этом случае для нахождения направления кориолисова ускорения достаточно повернуть вектор относительной скорости на угол 90° в сторону переносного вращения (рис. 106, b).
На основании формулы (18) можно указать следующие случаи, когда кориолисово ускорение равно нулю: 1) ωe = 0; 2) ωe//Vr; 3) Vr = 0. Второй и третий случаи могут возникать в процессе движения, но особого интереса не представляют. Первый случай имеет место, когда переносное движение поступательное, и часто встречается при решении конкретных вопросов теории и практических задач.
№13
-------- Кориолисово ускорение.
Поворотным ускорением (ускорением Кориолиса) называется составляющая абсолютного ускорения точки в составном движении, равная удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки: 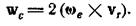
Появление поворотного ускорения обусловливается двумя причинами:
1) вследствие относительного движения точки, перемещающейся по отношению к подвижной системе отсчета, изменяется переносная скорость точки; 2) вследствие вращательного переносного движения дополнительно изменяется направление относительной скорости по отношению к неподвижной системе отсчета.
Например, если человек идет равномерно вдоль радиуса равномерно вращающейся платформы, то его относительной скоростью является скорость его движения вдоль радиуса, а переносной— скорость той точки платформы, где он находится в данный момент.
------------- Определение модуля и направления(Правило Жуковского)
Модуль поворотного ускорения определяется как модуль векторного произведения: 
Для определения направления поворотного ускорения удобно пользоваться правилом Жуковского:
Чтобы найти направление поворотного ускорения, следует спроектировать относительную скорость точки на плоскость, перпендикулярную оси переносного вращения, и повернуть эту проекцию в той же плоскости на 90°, в сторону переносного вращения
№14-15
----------- ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ т.т.
Плоскопараллельным или плоским называют движение твердого тела, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.
Плоское движение тел является одним из наиболее распространенных в технике. Плоское движение совершают тела качения (колеса, катки, цилиндры) на прямолинейном участке пути; отдельные детали механизмов, предназначенных для преобразования вращательного движения одного тела в поступательное или колебательное другого; шестерни планетарных передач.
В теории плоского движения тел доказывается несколько предложений.
1. Для описания плоского движения тел достаточно описать движение точек одного сечения тела плоскостью, параллельной неподвижной плоскости.
2. Движение тела может рассматриваться как результат сложения поступательного движения и вращения тела относительно одной из точек тела, называемой полюсом.
3. Характеристики вращательного движения тела при его плоском движении не зависят от выбора полюса.
------------ Теорема о сложении скоростей
Связь между относительной, переносной и абсолютной скоростями точки устанавливается следующей теоремой.
Теорема. Абсолютная скорость точки равна сумме переносной и относительной скоростей: 
------------------ Теорема о сложении ускорений (теорема Кориолиса)
Абсолютное ускорение точки равно сумме переносного, относительного и кориолисова ускорений: 
Можно сказать, что часть абсолютного ускорения — ускорение Кориолиса — связана с изменением абсолютной скорости, обусловленным двумя причинами: 1) влиянием переносного движения на относительную скорость; 2) влиянием относительного движения на переносную скорость
------------- Теорема о проекциях скоростей 2-х точек тела.
Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. 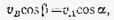
Теорема позволяет легко находить скорость данной точки тела, если известны направление скорости этой точки и скорость какой-нибудь другой точки того же тела.
Аналитический способ определения скоростей точек тела
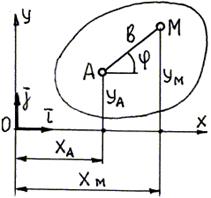
| При использовании аналитического метода считаются известными уравнения движения плоской фигуры (тела, совершающего плоскопараллельное движение):  (1)
Тогда координаты точки М (рис.) будут (1)
Тогда координаты точки М (рис.) будут
 (2) (2) 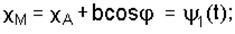 где b – расстояние от точки М до полюса А. где b – расстояние от точки М до полюса А.
|
Модуль скорости точки М определяется по формуле
 .
.
Направление вектора Vм определяется по направляющим косинусам:


Таким образом, задача по определению скоростей точек плоской фигуры сводится к известному решению соответствующей задачи кинематики точки.
Угловая скорость плоской фигуры определяется дифференцированием последнего уравнения из (1), т.е.
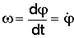 (3)
(3)
Аналитический метод решения задачи рекомендуется использовать в тех случаях, когда требуется определить скорости точек для большого числа положений плоской фигуры.
Аналитический способ определения ускорений точек тела
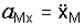
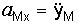 При использовании аналитического метода уравнения движения (1) плоской фигуры считаются известными. Дважды дифференцируя по времени выражения (2) координат точки М, получим проекции ускорения этой точки:
При использовании аналитического метода уравнения движения (1) плоской фигуры считаются известными. Дважды дифференцируя по времени выражения (2) координат точки М, получим проекции ускорения этой точки:
Модуль ускорения равен
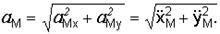 .
.
Направление ускорения определяется направляющими косинусами:
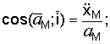 .
. 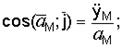
Таким образом, задача по определению ускорений точек сводится к соответствующей задаче кинематики точки.
Угловое ускорение тела находится дифференцированием третьего уравнения движения из (1)

№16-17
------------- ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ т.т. МЦС
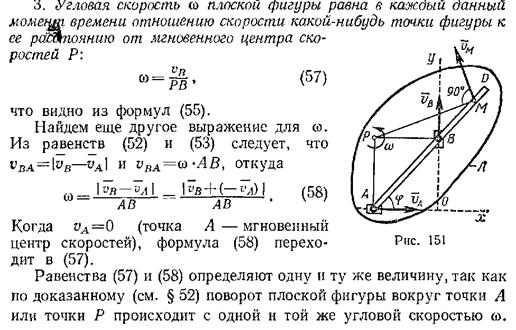
Мгновенный центр скоростей (М.Ц.С. и обозначают буквой Р) — точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело.
Доказательство следующее. Векторы скоростей точек плоскости, связанной с фигурой, определяются векторной суммой двух векторов, один из которых одинаков для всех точек плоскости, а другой зависит от положения точки на плоскости. Значит, на плоскости должна существовать точка, где вектор скорости во вращении относительно полюса равен по величине, но направлен противоположно вектору скорости полюса. Эта точка и будет иметь скорость, равную нулю, т.е. являться мгновенным центром скоростей.
------------Определение угловой скорости тела скоростей точек тела.
Скорость любой точки тела при плоском движении равна геометрической сумме скорости полюса и скорости во вращении точки относительно полюса.



------------ Общий случай нахождения МЦС--??????
1. При выборе в качестве полюса мгновенного центра скоростей величины и направления скоростей точек тела при его плоском движении определяются точно так же, как и при вращательном. Отличием является то, что для каждого момента движения тела положение мгновенной оси вращения необходимо находить. Соответственно необходимо находить и расстояния точек до этой оси.
2. Скорости всех точек фигуры при ее плоском движении пропорциональны их расстояниям до М.Ц.С. и перпендикулярны радиусам вращения - т.е. отрезкам, соединяющим точки с М.Ц.С.
3. Если уметь определять положение мгновенных центров скоростей звеньев плоских механизмов, то задачи на определение скоростей точек и угловых скоростей звеньев этих механизмов окажутся ничуть не сложнее аналогичных задач на вращательное движение связанных между собой тел.
----------Различные способы нахождения МЦС


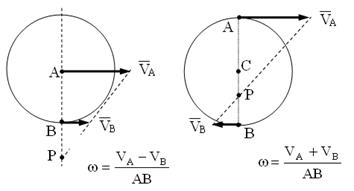 3. Случаи, когда векторы скоростей точек параллельны между собой и перпендикулярны отрезку, соединяющему точки.
3. Случаи, когда векторы скоростей точек параллельны между собой и перпендикулярны отрезку, соединяющему точки.
Эти случаи часто встречается, когда определяются угловые скорости тел качения М.Ц.С. находится на пересечении линии, соединяющей точки, и линии, соединяющей концы векторов скоростей точек. Величины скоростей точек в этом случае должны быть известны.
При противоположном направлении векторов скоростей М.Ц.С. расположен между точками, скорости которых известны; при одинаковом направлении - со стороны меньшей скорости и на продолжении отрезка, соединяющего точки.
Угловые скорости тел в этом случае по скоростям двух точек могут определяться сразу (следствие 2) по формулам, приведенным рядом с рисунками. Находить расстояния точек до М.Ц.С. в этом случае, если это не требуется для определения скоростей каких-либо других точек, необязательно.
Дата добавления: 2015-10-28; просмотров: 565 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теоремы о сложении скоростей точки и об абсолютной производной вектора. | | | Случай, когда векторы скоростей точек параллельны между собой и не перпендикулярны отрезку, соединяющему точки. |