Ускорение точки при векторном способе задания движения.

По определению ускорение является производной по времени от вектора скорости:

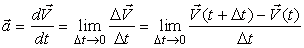(2)

Когда Δ 0, точка M1 M; плоскость, где лежат векторы (t), (t + Δt) и (Δt), содержащая две касательные к траектории в точках M и M1 (рис. 62), стремится занять положение 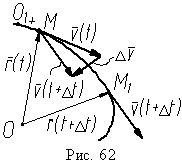соприкасающейся плоскости в точке M; сам вектор направлен в сторону вогнутости траектории.

Таким образом, вектор ускорения a лежит в соприкасающейся плоскости и всегда направлен в сторону вогнутости траектории.

Очевидно, что a является ускорением в данное мгновение времени или мгновенным ускорением, а средним ускорением за промежуток времени Δt называется отношение ΔV / Δt. Соответственно, размерностью ускорения будет м / с2 (ме тр за секунду в квадрате).

8. Вращательное движение твердого тела вокруг неподвижной оси. Уравнение движения, угловая скорость и угловое ускорение т.т.

Движение тела с двумя неподвижными точками (вращение тела вокруг неподвижной оси).

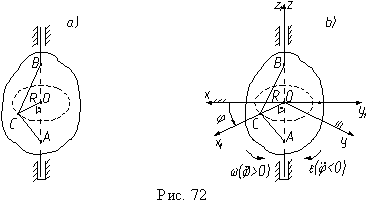
При вращении тела вокруг неподвижной оси две его точки, например A и B, лежащие на оси вращения, остаются неподвижными (рис 72, a).

Так как точки A и B кинематической модели неподвижны, то движение одной ее подвижной точки C определяет движение всех точек твердого тела, вращающегося вокруг неподвижной оси.

В частности (рис. 72, a), мы видим, что точка C движется по окружности радиуса OC = R, который называется радиусом вращения, в плоскости, перпендикулярной оси вращения. Следовательно, траекториями всех точек тела, не лежащих на оси вращения, являются окружности соответствующих радиусов, которые лежат в плоскостях, перпендикулярных оси вращения.

Кроме того, положение всех точек тела определяется тремя координатами точки C. Но эти три параметра связаны между собой двумя уравнениями постоянства длины отрезков AC и BC. То есть среди параметров только один независимый. Следовательно, твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы, которую в кинематике твердого тела называют вращательной или угловой степенью свободы.

Дата добавления: 2015-10-28