
Читайте также:
|
Принцип возможных перемещений: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на неё активных сил при любом возможном перемещении системы была равна нулю. Математически сформулированное условие равновесия выражается равенством  =0, которое называют также уравнением возможных работ. Это равенство можно ещё представить в аналитической форме.
=0, которое называют также уравнением возможных работ. Это равенство можно ещё представить в аналитической форме.
Принцип возможных перемещений устанавливает общее условие равновесия механической системы, не требующее рассмотрения равновесия механической системы, не требующее рассмотрения равновесия отдельных частей (тел) этой системы и позволяющее при идеальных связях исключить из рассмотрения все наперёд неизвестные реакции связей.
19. ОБОБЩЁННЫЕ КООРДИНАТЫ. ОБОБЩЁННАЯ СКОРОСТЬ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ. ОБОБЩЁННАЯ СИЛА
Независимые параметры qi (i=1, 2,..., s) любой размерности, число которых равно числу s степеней свободы механической системы и которые однозначно определяют положение системы. Закон движения системы в обобщ. координатах даётся s ур-ниями вида qi=qi(t), где t — время. Обобщ. коорд. пользуются при решении мн. задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число ур-ний, описывающих движение системы, по сравнению, напр., с ур-ниями в декартовых координатах.
Число степеней свободы в механике - число независимых между собой возможных перемещений механич. системы. Число степ. своб. зависит от числа матер. точек, образующих систему, а также от числа и хар-ра наложенных на систему связей механических. Для свободной матер. точки число степ. своб. равно 3, для свободного твёрдого тела — 6, для тела, имеющего неподвижную ось вращения, равно 1. Для любой голономной системы (системы с геом. связями) число степ. своб. равно числу s независимых между собой координат, определяющих положение системы, и даётся равенством s=3n-k, где n — число точек системы, k — число геом. связей. Для неголономной системы число степ. своб. меньше числа координат, определяющих положение системы, на число кинематич. связей, не сводящихся к геометрическим.
Обобщённые силы - величины, играющие роль обычных сил, когда при изучении равновесия или движения механич. системы её положение определяется обобщёнными координатами. Число обобщ. сил равно числу s степеней свободы системы; при этом каждой обобщённой координате qi соответствует своя обобщ. сила Qi. Значение обобщ. силы Q1, соответствующей координате q1, можно найти, вычислив элем. работу dA1 всех сил на возможном перемещении системы, при к-ром изменяется только координата q1:, получая приращение dq1. Тогда dA1=Q1dq1т. е. коэффициент при dqi в выражении dA1 и будет обобщённой силой Q1. Аналогично вычисляются Q2, Q3,..., Qs. Размерность обобщ. силы зависит от размерности обобщённой координаты.
Обобщённая скорость. При движении системы ее обобщенные координаты непрерывно изменяются с течением времени, т.е. являются функциями времени:
q1=q1(t), q2=q2(t),......,qs(t) (1)
Уравнения (1) представляют собой кинематические уравнения движения механической системы в обобщенных координатах.
Производные от обобщенных координат по времени называются обобщенными скоростями системы:

Размерность обобщенной скорости зависит от размерности соответствующей обобщенной координаты. Если q - линейная величина в метрах, то - обычная линейная скорость в м/c, если q - угол в радианах, то - угловая скорость в рад/с и т.д.
20. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Имеем систему несвободных материальных точек, движущихся с теми или иными ускорениями под действием активных, то есть заданных сил. Если к каждой из точек, кроме вышеуказанных сил и сил реакций связей добавить ее силу инерции, то получаемая система сил в соответствии с принципом Даламбера будет уравновешенной.
А для уравновешенной системы сил уже в соответствии с принципом возможных перемещений сумма виртуальных работ сил на любом возможном перемещении системы должна быть равна нулю.

Формулировка:
В любой момент движения механической системы с идеальными связями сумма виртуальных работ активных сил и сил инерции на любом возможном перемещении системы равна нулю.
Это равенство принято называть общим уравнением динамики или принципом Лагранжа-Даламбера.
21. УРАВНЕНИЕ ЛАГРАНЖА II РОДА. ОБОБЩЁННАЯ ЗАДАННАЯ СИЛА И ОБОБЩЁННАЯ СИЛА ИНЕРЦИИ
Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения движения системы в обобщенных координатах.
Обобщенные координаты – независимые между собою переменные параметры системы, однозначно определяющие положение системы в любой момент времени. Число обобщенных координат системы с голономными связями равно числу ее степеней свободы.
Уравнения Лагранжа имеют вид
 , i = 1, 2,…,n, (1.1)
, i = 1, 2,…,n, (1.1)
где n – число степеней свободы голономной системы; qi – обобщенные координаты;  – обобщенные скорости (производные обобщенных координат по времени t); Qi – обобщенные силы; T – кинетическая энергия системы;
– обобщенные скорости (производные обобщенных координат по времени t); Qi – обобщенные силы; T – кинетическая энергия системы;  и
и  – частные производные кинетической энергии системы по обобщенной координате qi и по обобщенной скорости
– частные производные кинетической энергии системы по обобщенной координате qi и по обобщенной скорости  ;
;
 – производная
– производная  по времени t.
по времени t.
Кинетическую энергию системы со стационарными связями целесообразно до подстановки в уравнения (1.1) представить в виде функций обобщенных координат и обобщенных скоростей
 (1.2)
(1.2)
Обобщенные силы.
Каждой обобщенной координате можно вычислить соответствующую ей обобщенную силу Qk.
Вычисление производится по такому правилу.
Чтобы определить обобщенную силу Qk, соответствующую обобщенной координате qk, надо дать этой координате приращение  (увеличить координату на эту величину), оставив все другие координаты неизменными, вычислить сумму работ всех сил, приложенных к системе, на соответствующих перемещениях точек и поделить ее на приращение координаты
(увеличить координату на эту величину), оставив все другие координаты неизменными, вычислить сумму работ всех сил, приложенных к системе, на соответствующих перемещениях точек и поделить ее на приращение координаты  :
:

где –  перемещение i-той точки системы, полученное за счет изменения k–той обобщенной координаты.
перемещение i-той точки системы, полученное за счет изменения k–той обобщенной координаты.
Обобщенная сила определяется с помощью элементарных работ. Поэтому эту силу можно вычислить иначе:

И так как  есть приращение радиуса-вектора
есть приращение радиуса-вектора 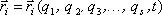 за счет приращения координаты при остальных неизменных координатах и времени t, отношение
за счет приращения координаты при остальных неизменных координатах и времени t, отношение 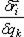 можно определять как частную производную
можно определять как частную производную  . Тогда
. Тогда

где координаты точек – функции обобщенных координат.
Если система консервативная, то есть движение происходит под действием сил потенциального поля, проекции которых 

 , где
, где  , а координаты точек – функции обобщенных координат, то
, а координаты точек – функции обобщенных координат, то

Обобщенная сила консервативной системы есть частная производная от потенциальной энергии по соответствующей обобщенной координате со знаком минус.
Конечно, при вычислении этой обобщенной силы потенциальную энергию следует определять как функцию обобщенных координат
П = П(q1, q2, q3,…,qs).
Замечания.
Первое. При вычислении обобщенных сил реакции идеальных связей не учитываются.
Второе. Размерность обобщенной силы зависит от размерности обобщенной координаты.
Обобщенные силы инерции.
По той же методике, по которой вычислялись обобщенные силы Qk, соответствующие активным, задаваемым, силам, определяются и обобщенные силы Sk, соответствующие силам инерции точек системы:

И, так как  то
то 
Немного математических преобразований.
Очевидно, 
Отсюда  .
.
Так как  а qk = qk(t), (k = 1,2,3,…, s), то
а qk = qk(t), (k = 1,2,3,…, s), то
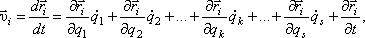 где
где 
Значит, частная производная скорости  по
по 
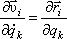
Кроме того, в последнем члене можно поменять порядок дифференцирования:
. 
Получаем
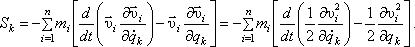
Разделив последнюю сумму на две и, имея ввиду, что сумма производных равна производной от суммы, получим

где  – кинетическая энергия системы,
– кинетическая энергия системы, 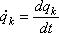 - обобщенная скорость.
- обобщенная скорость.
Дата добавления: 2015-10-28; просмотров: 221 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод кинетостатики. | | | jet propulsion research group |