
|
Читайте также: |
 Вектор скорости v точки направлен по касательной к траектории и определяется одной проекцией
Вектор скорости v точки направлен по касательной к траектории и определяется одной проекцией 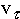 , равной первой производной от криволинейной координаты s этой точки по времени:
, равной первой производной от криволинейной координаты s этой точки по времени:
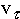 = ds / dt =
= ds / dt =  .
.
Величину 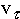 , которая может быть как положительной, так и отрицательной, называют числовым ( или алгебраическим) значением скорости.
, которая может быть как положительной, так и отрицательной, называют числовым ( или алгебраическим) значением скорости.
Модуль скорости v = | 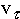 | и, следовательно, значения v и
| и, следовательно, значения v и 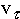 могут отличаться лишь знаком:
могут отличаться лишь знаком:
v = 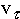 , если точка движется в положительном направлении отсчета координаты s, или
, если точка движется в положительном направлении отсчета координаты s, или
v = - 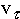 , если точка движется в противоположном направлении.
, если точка движется в противоположном направлении.
Таким образом, величина 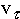 определяет одновременно и модуль скорости, и сторону, в которую направлен вектор v вдоль касательной.
определяет одновременно и модуль скорости, и сторону, в которую направлен вектор v вдоль касательной.
Мгновенным ускорением (или просто ускорением)  тела называют предел отношения малого изменения скорости
тела называют предел отношения малого изменения скорости  к малому промежутку времени Δ t, в течение которого происходило изменение скорости:
к малому промежутку времени Δ t, в течение которого происходило изменение скорости:
|
Направление вектора ускорения  в случае криволинейного движения не совпадает с направлением вектора скорости
в случае криволинейного движения не совпадает с направлением вектора скорости  Составляющие вектора ускорения
Составляющие вектора ускорения  называют касательным (тангенциальным)
называют касательным (тангенциальным)  и нормальным
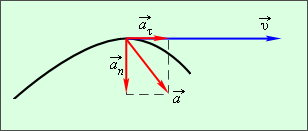
и нормальным  ускорениями (рис. 1.1.5).
ускорениями (рис. 1.1.5).
|
| Рисунок 1.1.5. Касательное и нормальное ускорения |
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:

|
Вектор  направлен по касательной к траектории.
направлен по касательной к траектории.
Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).

|
| Рисунок 1.1.6. Движение по дугам окружностей |
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:

|
Вектор  всегда направлен к центру окружности (см. §1.6).
всегда направлен к центру окружности (см. §1.6).
Пусть движение задано в прямоугольной системе координат Oxyz, которую мы принимаем за неподвижную, и нам известны законы изменения координат точки: x = x(t); y = y(t); z = z(t).
дифференцируем, учитывая, что единичные векторы осей координат постоянны:
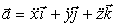
| (2) |
Проекциями вектора ускорения на оси координат являются сомножители перед единичными векторами в равенстве (2), следовательно,

| (3) |
Зная проекции ускорения на оси координат, можно определить величину вектора ускорения:

| (4) |
Направляющие косинусы, определяющие направление вектора ускорения в системе координат, будут равны

| (5) |
Формулу (2) можно использовать для геометрического построения вектора ускорения. Представляя вектор ускорения как сумму трех взаимно перпендикулярных составляющих

| (6) |
где

| (7) |
а затем геометрически сложив их, найдем вектор ускорения. При построении составляющих по формулам (7) нужно учитывать знаки вторых производных координат точки. Если они положительны, то направления составляющих совпадают с направлениями единичных векторов, если они отрицательны, то составляющие направлены в противоположную сторону.
Дата добавления: 2015-10-28; просмотров: 192 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Уравнения равновесия плоской произвольной, параллельной и сходящейся систем сил. | | | Ускорение точки при векторном способе задания движения. |