Теорема об изменении кинетической энергии материальной точки.

Работой силы F на конечном перемещении точки ее приложения является

скалярное произведение этой силы на вектор перемещения: dA = Fdr =

Fdr*cosα = F_xdx + F_ydy. Теорема:

Единственной причиной изменения кинетической энергии объекта является

приложенная к нему внешняя сила: dT = d(mV²/2) = (2mVdV)/2 = Fdr =

dA. dT=dA – мерой действия силы при изменении

кинетической энергии объекта является производимая внешними силами работа.

T1 –T0 =A – изменение кинетической энергии

материального объекта на некотором перемещении равно работе сил, приложенных к

нему, на том же перемещении.

Работа сил тяжести. Пусть 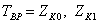, координаты начального и конечного положения точки k тела. Работа силы тяжести действующих на эту частицу веса 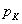будет 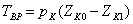. Тогда полная работа:

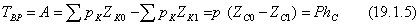где Р - вес системы материальных точек, 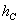- вертикальное перемещение центра тяжести С.

Работа силы равна произведению модуля силы на перемещение и на косинус угла между ними.

Сила тяжести выражается через массу тела по формуле G = mq. Она приложена к телу в центре масс. Работа силы тяжести при опускании центра масс положительна, при поднимании - отрицательна. Работа силы тяжести за полный цикл движения механизма равна нулю.

Теорема о работе силы: Работа равнодействующей силы равна алгебраической сумме работ составляющих сил на том же перемещении А=А₁+А₂+…+А_n.

Работа силы тяжести:, >0, если начальная точка выше конечной.

Работа силы упругости: –работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.

а) сила упругости ,где k — коэффициент упругости (в случае пружины применяется также название — жесткость); х — абсолютная деформация;

б) сила тяжести ;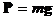

13.Работа силы и момента силы.

Момент силы - это мера вращающего действия силы на тело. Он определяется произведением силы на ее плечо. F-сила, r-радиус

Момент силы обычно считают положительным, когда сила вызывает поворот тела против часовой стрелки, и отрицатель­ным при повороте по часовой стрелке.

Чтобы сила могла проявить свое вращающее действие, она должна иметь плечо. Иначе говоря, она не должна прохо­дить через ось вращения.

Определение силы или момента силы, если известна мас­са или момент инерции, позволяет узнать только ускорение, т.е. как быстро изменяется скорость. Надо еще узнать, на­сколько именно изменится скорость. Для этого должно быть известно, как долго была приложена сила. Иначе говоря, сле­дует определить импульс силы (или ее момента).

Работа силы - это мера действия силы на тело при некотором его перемещении под действием этой силы. Она равна произведению модуля силы и перемещения точки при­ложения силы.

Если сила направлена в сторону движения (или под ост­рым углом к этому направлению), то она совершает положи­тельную работу, увеличивая энергию движения тела. Когда же сила направлена навстречу движению (или под тупым углом к его направлению), то работа силы отрицательная и энергия движения тела уменьшается.

Работа момента силы — это мера воздействия момента силы на тело на данном пути (во вращательном движении). Она равна произведению модуля момента силы и угла поворота.

Понятие работы представляет собой меру внешних воз­действий, приложенных к телу на определенном пути, вызы­вающих изменения механического состояния тела.

14. Принцип Даламбера для м.т. и механической системы. Силы Даламбера.

Д’Аламбера принцип — в механике: один из основных принципов динамики, согласно которому, если к заданным (активным) силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил.

ринцип Даламбера:
Материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равновесии:

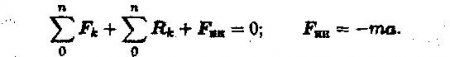
Принцип Даламбера. При движении материальной точки активные силы и силы реакции связей вместе с силой инерции точки образуют равновесную систему сил.

Принцип Даламбера называют еще методом кинетостатики. Задачи динамики с помощью этого метода сводятся к задачам статики.

Принцип Даламбера - при движении механической системы активные силы, реакции связей и силы инерции образуют равновесную систему сил в любой момент движения.

Д’Аламберовы силы инерции

В принципе д’Аламбера в рассмотрение вводятся подлинно отсутствующие в природе силы инерции, которые невозможно измерить никакой физической аппаратурой. Эти силы вводятся ради использования искусственного математического приёма, основанного на применении принципа Д’Аламбера в формулировке Лагранжа, где задача на движение с помощью введения сил инерции формально сводится к проблеме равновесия

15.Принцип Даламбера для механической системы. К чему приводятся силы инерции при поступательном и вращательном движениях т.т. (записать формулы).

Принцип Даламбера - при движении механической системы активные силы, реакции связей и силы инерции образуют равновесную систему сил в любой момент движения.

При поступательном движении системы все ее точки проходят одинаковые пути, имеют в данный момент времени одинаковые скорости и ускорения. При вращательном движения твердого тела все эти характеристики различны для разных точек вращающегося тела, поэтому и математическая форма 2-го закона Ньютона будет иной. При вращательном движении существенно изменяются сами понятия причины, вызывающей вращение, и величины, определяющей инертность тела.\

Если точка массой m, находясь под действием постоянной силы F в течение t сек, двигается прямолинейно, то теорема об изменении количества движения (Е. М. Никитин, § 89) выражается формулой
(1) mv - mv₀ = Ft,
где разность mv-mv₀ – величина изменения проекции количества движения на ось, совпадающую с направлением движения, а произведение Ft – проекция импульса силы на ту же ось.

В СИ количество движения и импульс силы измеряются в ньютон-секундах (Н*с).

Если, рассматривая действие силы F на материальную точку массой m, учитывать не продолжительность ее действия, а протяженность, т. е. то расстояние, на котором действует сила, то получим теорему об изменении кинетической энергии точки (Е. М. Никитин, § 91):
(2) mv²/2 - mv₀²/2 = A,
где A – работа всех сил, приложенных к точке, а mv₀²/2 и mv²/2 – кинетическая энергия точки соответственно в начале и конце действия сил.

Кинетическая энергия измеряется единицами работы, т. е. в СИ – в джоулях (Дж).

При поступательном движении динамическими характеристиками являются сила, масса, импульс. При вращательном движении динамическими характеристиками являются момент силы, момент инерции, момент импульса. Эти характеристики можно рассматривать относительно точки вращения (полюса) и относительно оси вращения. В дальнейшем будем рассматривать эти характеристики относительно оси вращения. Определим эти характеристики.

В этом уравнении, выражающем основной закон динамики для вращательного движения тела, множителем пропорциональности является момент инерции тела. Тело с большим моментом инерции труднее привести во вращение.

Кинетическая энергия вращающегося тела
E_вр = Jω²/2.

Если тело находится в плоскопараллельном движении, например, катящееся колесо, то его кинетическая энергия складывается из двух слагаемых:
E_об = mv²/2 + Jω²/2,
где mv²/2 – кинетическая энергия, получающаяся от поступательной части этого сложного движения (см. § 37) при скорости v, равной скорости центра тяжести тела, а Jω²/2 – кинетическая энергия от вращательной части, причем J – момент инерции относительно оси, проходящей через центр тяжести тела.

Дата добавления: 2015-10-28