Метод кинетостатики.

Даламберова сила инерции не имеет источника своего возникновения - другого тела. Она вводится условно в ходе математических преобразований основного уравнения динамики, чтобы придать уравнениям динамики вид условия или уравнения равновесия.

Следовательно, прикладывая силу инерции к движущейся материальной точке, мы можем говорить лишь об условном равновесии, приложенных к ней сил. Однако такое понимание динамического уравнения движения позволяет, используя уравнения равновесия статики, составлять динамические уравнения. Этот метод составления уравнений движения и называется методом кинетостатики.

Принцип Даламбера для механической системы.

Рассмотрим теперь механическую систему, состоящую из n материальных точек. Выделим какую-нибудь из точек системы с массой m. Под действием приложенных к ней внешних и внутренних сил (в которые входят и активные силы, и реакции связей) некоторым ускорением Введя для этой точки силу инерции

, получим согласно равенству F ̅ª+ + 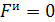, что , , образуют уравновешенную систему сил.

Принцип Даламбера для механической системы: если в любой момент времени из точек системы кроме действующих на нёё внешних и внутренних сил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применять все уравнения статики.

К чему приводится силы инерции при плоскопараллельном движении т.т.

Если тело имеет плоскость симметрии и движется параллельно этой плоскости, то, очевидно, система сил инерции тела приведётся к лежащим в плоскости симметрии силе, равной и приложенной в центре масс С тела, и паре с моментом где угловое ускорение тела. При решении задач вычисляется модуль момента , а его направление противоположное , указывается на чертеже.

18.

Возможные или виртуальные перемещения .

Возможные или как их ещё называют, виртуальные, перемещения должны удовлетворять двум условиям: 1) быть элементарными, так как при конечном перемещении система может прийти в положение, где эффект наложенных связей будет другим; 2) быть такими, чтобы все наложенные в данный момент времени на систему связи сохранялись, иначе может изменится вид рассматриваемой механической системы.. Таким образом, возможным перемещением механической системы будем называть любую совокупность элементарных перемещений точек этой системы из занимаемого в данный момент времени положения, которые допускаются всеми наложенными на систему связями. При этом под допускаемыми в случае неудерживающих связей будем понимать те возможные перемещения, при которых связи сохраняются (точки системы от связей не «освобождаются»)

---

Дата добавления: 2015-10-28