Уравнения равновесия плоской произвольной, параллельной и сходящейся систем сил.

РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ

Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая, а следовательно, и главный вектор этих сил были равны нулю.

1. Геометрическое условие равновесия.

для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.

2. Аналитические условия равновесия. Аналитически модуль главного вектора системы сил определяется формулой

R обратится в нуль только тогда, когда одновременно Rx=0, Ry=0, Rz=0, т. е., когда действующие на тело силы будут удовлетворять равенствам:

Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил. В случае плоской системы сходящихся сил получим только два условия равновесия:

РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ.

Необходимые и достаточные условия равновесия любой системы сил даются равенствами R=0 и Mо=0.

1. Основная форма условий равновесия. Так как вектор R равен нулю, когда равны нулю его проекции Rx и Ry, то для равновесия должны выполняться равенства Rx=0, Ry=0 и Мо—0, где в данном случае Мо — алгебраический момент, а О — любая точка в плоскости действия сил. предыдущие равенства будут выполнены, когда действующие силы удовлетворяют условиям:

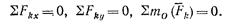(1)

Формулы 1 выражают: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

2*. Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось Ох, не перпендикулярную прямой АВ, были равны нулю:

2

3*. Третья форма условий равновесия (уравнения трех моментов): для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю:

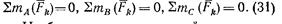3

Равновесие плоской системы параллельных сил. В случае, когда все действующие на тело силы параллельны друг другу, можно направить ось Ох перпендикулярно силам. а ось Оу параллельно им. Тогда проекция каждой из сил на ось Ох будет равна нулю и первое из равенств 1 обратится в тождество вида 0=0. В результате для параллельных сил останется два условия равновесия:

где ось Оу параллельна силам.

Другая форма условий равновесия для параллельных сил, получающаяся из равенств 30), имеет вид:

При этом точки А и В не должны лежать на прямой, параллельной силам.

13.Уравнения равновесия пространственной произвольной, параллельной и сходящейся систем сил.

для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ.

Необходимые и достаточные условия равновесия любой системы сил выражаются равенствами R=0, Mo=0 Но векторы R и Мо равны нулю только тогда, когда Rx=Ry=Rz=Q и Мх= =My=Mz=0, т.е. когда действующие силы будут удовлетворять условиям:

Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.

Если на тело кроме сил действует еще пара, заданная ее моментом т, то при этом вид первых трех из условий 51) не изменится (сумма проекций сил пары на любую ось равна нулю), а последние три условия примут вид:

Случай параллельных сил. В случае, когда все действующие на тело силы параллельны друг другу, можно выбрать координатные оси так, что ось z будет параллельна силам Тогда проекции каждой из сил на оси х и у и их моменты относительно оси z будут равны нулю и система 51)

даст три условия равновесия:

Остальные равенства обратятся при этом в тождества вида 0=0.

Следовательно, для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную силам, и суммы их моментов относительно двух других координатных осей были равны нулю.

КИНЕМАТИКА

1. Что изучает кинематика

Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.

Задачи кинематики
Главной задачей кинематики является математическое (уравнениями, графиками, таблицами и т. п.) определение положения и характеристик движения точек или тел во времени. Любое движения рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).

1. Траектория точки.

Траекторией материальной точки называется линия, описываемая пространстве этой точкой при ее движении. В зависимости от формы траектории различают прямолинейное и криволинейное движения точки. Если все участки траектории точки лежат в одной плоскости, то движение точки называют плоским.

Траектория точки – непрерывная кривая, которую описывает точка при своем движении.

1. Способы задания движения материальной точки

Задать движение точки означает задать ее положение в каждый момент времени. Положение это должно определяться в какой-либо системе координат. Однако для этого не обязательно всегда задавать сами координаты; можно использовать величины, так или иначе с ними связанные. Ниже описаны три основных способа задания движения точки.

1. Естественный способ. Этим способом пользуются, если известна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве. При естественном способе необходимо задать:

а) траекторию движения (относительно какой-либо системы координат);

б) произвольную точку на ней нуль, от которого отсчитывают расстояние S до движущейся частицы вдоль траектории;

в) положительное направление отсчета S (при смещении точки М в противоположном направлении S отрицательно);

г) начало отсчета времени t;

д) функцию S(t), которая называется законом движения точки.

2. Координатный способ. Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание:

а) системы координат (не обязательно декартовой) q1, q2, q3;

б) начало отсчета времени t;

в) закона движения точки, т.е. функций q1(t), q2(t), q3(t).

Говоря о координатах точки, мы всегда будем иметь в виду (если не оговорено противное) ее декартовы координаты.

3. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку. В этом случае для описания движения необходимо задать:

а) начало отсчета радиус-вектора r;

б) начало отсчета времени t;

в) закон движения точки r (t).

Поскольку задание одной векторной величины r эквивалентно заданию трех ее проекций x, y, z на оси координат, от векторного способа легко перейти к координатному. Если ввести единичные векторы i, j, k (i = j = k = 1), направленные соответственно вдоль осей x, y и z (рис. 2), то, очевидно, закон движения может быть представлен в виде:

r (t) = x(t) i +y(t) j +z(t) k. (1)

Дата добавления: 2015-10-28