Регрессионный метод идентификации линейных систем (Метод наименьших квадратов)

Рассмотрим уравнение:

, (2.1)

В уравнении заменим производную конечной разностью:

, (2.2)

, (2.3)

, (2.4)

Подставим выражения (2.2)-(2.4) в уравнение (2.1):

, (2.5)

Приведя подобные, получим:

, (2.6)

Представим (2.6) в виде:

, (2.7)

где

.

Рассматриваемый метод идентификации, основан на регрессионных процедурах с использованием метода наименьших квадратов.

Рассматриваем систему, которая задана уравнением:

Минимизируемая функция имеет вид:

(2.8)

Запишем систему уравнений для нахождения , для этого найдем частные производные: 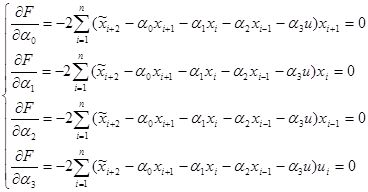(2.9)

(2.10)

Запишем систему в матричной форме:

(2.11)

. (2.12)

По полученным найдем коэффициенты а_i

.

1. Градиентные методы идентификации нелинейных систем

Для общей задачи минимизации функционала

при ограничениях

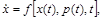
где f – нелинейная вектор - функция

Случай p_i - const будем задаваться начальным значением pⁱ, i- номер итерации, и решив систему дифференциальных уравнений оценим величину функции штрафа Jⁱ. Слегка изменяя pⁱ, для нового значения найдем штраф

Jⁱ +h_j, j = 1,n, n - число неизвестных коэффициентов

j-ю компоненту вектора-градиента функции штрафа можно приближенно оценить как

(3)

Повторяя эту процедуру для возмущений различных компонент вектора параметров, определим приближенное значение вектора-градиента dJ/dpⁱ Первое приращение вектора параметров в направлении наискорейшего спуска к минимуму функции штрафа составит

(4)

и Kⁱ – выбирается из условия

(5)

а новое приближение для вектора параметров определится как

pⁱ⁺¹ = pi +Dpⁱ.

Простота приближенного метода позволила положить его в основу нескольких итерационных схем, однако трудно оценить ошибку, связанную с приближенным вычислением dJ/dpⁱ (процедура точного вычисления свелась бы к уже известным алгоритмам решения динамических задач). Приближенная процедура приводит к существенным ошибкам, особенно тогда, когда функция штрафа не очень чувствительна к изменению вектора параметров. Последнее, к сожалению, довольно часто имеет место, если измерения или наблюдения искажены помехой и имеются неизвестные входные сигналы.

Алгоритм вычислений следующий

1.Задаемся начальными значениями вектора параметров р.

2.Решаем дифференциальные уравнения (2)

3.Вычисляем значения функционала (1)

4.Вычисляем компоненты вектора-градиента функционала (1) по ф.(3).

5.Определяем новые значения р по ф.4 из условия (5)

6.Переходим к п.2 алгоритма, если компоненты вектора-градиента больше некоторой величины e.

2. Коэффициенты системы есть функции времени, т.е. р = p(t).

Способы аппроксимации функции p(t).

Кусочно-постоянными функциями.

Кусочно-линейными функциями.

р

t

Полиномиальная гипроксимация.

4.Сплайн-аппроксимация.

где

p

Дата добавления: 2015-10-24