Модель третьего типа

Системе с кривой разгона третьего типа соответствует передаточная функция:

(26)

Представим структуру системы в виде последовательного соединения двух звеньев. Первое звено – реальное дифференцирующее, а второе – звено II-го порядка общего вида.

При подаче на вход первого звена единичного возмущения x(t)=1(t), выход звена , где δ=α₁b₁. Кривая разгона в этом случае является решением дифференциального уравнения:

(27)

Учитывая, что в точке перегиба(t=t_n) y^''(t_n)=0, уравнение (27) преобразуется к виду:

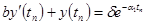(28)

Интегрируя (27) в пределах от t₁=0 до t₂=∞, получим:

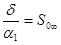(29)

При интегрировании (27) от t₁=t_m до t₂=∞ будем иметь:

(30)

Из соотношений (29) и (30)находим:

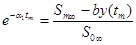(31)

а из (28) (29)получим

(32)

Решение системы из уравнений (31) и (32) даёт значения α₁ и b.

Если проинтегрировать уравнение (27) от точки перегиба кривой разгона до t=∞, получим:

, откуда, учитывая (29)

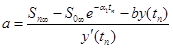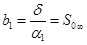; (33)

Исходные коэффициенты a_i вычисляются по формулам (5). Найденные коэффициенты проверяются решением дифференциального уравнения (27). Решение этого уравнения зависит от корней характеристического уравнения:

ar²+br+1=0.

При этом значение коэффициента с₁ одинаково для любого значения корней:

Варианты значений корней:

9. Вещественные неравные корни: r₁=α₂, r₂=α₃

где ;

(константы определены с учётом того, что все выкладки производились при нулевых начальных условиях: y(0)=0; y^'(0)=0)

10. Вещественные равные корни: r₁=r₂= -α₂

;

11. Комплексные корни: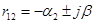

;

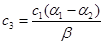
На основе изложенного метода идентификации моделей в виде дифференциального уравнения (передаточной функции) по кривой разгона можно установить следующую последовательность действий:

12. Определение принадлежности кривой разгона к одному из типов, рассматриваемых в методике.

13. Для всех кривых, кроме последнего типа устанавливается относительный масштаб по ординате, соответствующий y_уст=1 и вычерчивается приведенная кривая разгона.

14. По приведенной кривой разгона определяются значения:

t_n, t_m, y(t_n), y(t_m), y^'(t_n), S_0∞, S_n∞, S_m∞

15. Из соответствующих уравнений определяются значения α₁ и b.

16. Для кривых типа II и III определяются значения δ.

17. В зависимости от типа кривой по соответствующим формулам определяют коэффициент а.

18. Определяются коэффициенты дифференциального уравнения а₁, а₂, а₃ из соотношений (5). Для кривых типа II и III определяют значение b₁.

19. Определяются постоянные интегрирования в зависимости от типа.

20. Производится проверка с помощью графического построения, проверяется решение дифференциального уравнения.

Дата добавления: 2015-10-24