Модель первого типа

Передаточная функция системы первого типа:

, (4)

Представим структуру системы в виде последовательного соединения двух звеньев. Первое звено – апериодическое, а второе – в общем случае звено II-го порядка.

Приравняв исходную ПФ и полученную для последовательного соединения двух звеньев, легко установить связь между их коэффициентами:

; ; ; (5)

Так как звенья включены последовательно, то при подаче на вход воздействия в виде единичного скачка 1(t), вход во второе звено, равный выходу первого, определяется, как y_пр=1-exp(-α₁t), а выход второго звена будет представлять собой кривую разгона объекта.

Дифференциальное уравнение объекта можно записать:

ay^''+by^'+y=1-exp(-α₁t). (6)

Выразим b. Известно, что в точке перегиба графика функции вторая производная равна 0: y^''(t_п)=0. Тогда для момента времени, соответствующего точке перегиба (см. рисунок), уравнение (6) запишется:

a*0+b*y^'(t_п)+y(t_п)=1-exp(-α₁t_п),

откуда получим: (7)

Для нахождения неизвестных коэффициентов a и α₁ запишем (6) в виде: ay^''+by^'+exp(-α₁t)=1-y, (8).

Проинтегрируем (7) в пределах [t₁;t₂]:

(9)

S₁,₂ – площадь, ограниченная линией установившегося значения у, кривой разгона и вертикалями в точках t₁ и t₂:

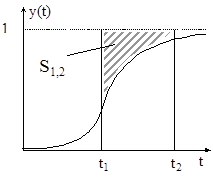
В уравнении (9) возьмём в качестве пределов интегрирования t₁=0, t₂= ∞. Тогда, учитывая, что:

y(0)=0; y^'(0)=0; y(∞)=1; y^'(∞)=0, получим:

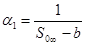(10)

S_0∞ - это площадь над кривой разгона для t₁=0 и t₂= ∞, то есть во всем диапазоне наблюдения.

Уравнения (7) и (10) образуют систему с двумя неизвестными: b и α₁. Решая эту систему (численно, графически, с помощью номограмм) мы можем определить значения этих коэффициентов.

Возьмём в (9) t₁=t_n, t₂=∞.Учитывая, что y(∞)=1; y^'(∞)=0, S_n∞ - площадь над кривой разгона для t₁=t_n и t₂= ∞ получим:

(11)

Подставляя значения a, b и α₁ в (5), получим значения коэффициентов a₃, a₂, a₁.

Достоинством этой методики является тот факт, что мы можем получить аналитическое выражение переходной функции, решить обратную задачу и оценить точность идентификации. Решение уравнения (6) может быть использовано для проверки соответствия найденных коэффициентов.

Решение дифференциального уравнения складывается из суммы общего решения однородного уравнения ay^''+by^'+y=0 и частного решения неоднородного.

Частное решение неоднородного уравнения имеет вид

, где (12)

Общее решение однородного уравнения зависит от корней характеристического уравнения:

ar²+br+1=0.

Варианты значений корней:

6. Вещественные неравные корни: r₁=α₂, r₂=α₃

, (y₀ - решение общего однородного уравнения)

где 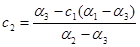; (13)

7. Вещественные равные корни: r₁=r₂= -α₂

; (14)

8. Комплексные корни:

; (15)

Дата добавления: 2015-10-24