Постановка задачи. Для объекта идентификации получают кривую разгона при входном воздействии в виде

Для объекта идентификации получают кривую разгона при входном воздействии в виде единичного скачка.

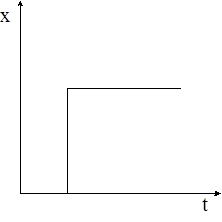
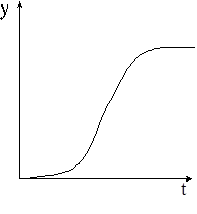
Входное воздействие Кривая разгона

Модель объекта будем искать в виде передаточной функции:

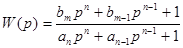, n>m

Надо определить а_i, b_i.

Если кривая разгона задана в реальных единицах, то для удобства обработки эту кривую разгона нормируют:

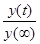получим кривую в диапазоне [0;1]

Связь между коэффициентами а_i, b_i и параметрами кривой разгона может быть установлена через систему уравнений:

a₁=F₁+b₁

a₂=F₂+b2+b₁F₁

a₃=F₃+b₃+b₂F₁+b₁F₂

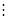
Параметры F_i, входящие в эту систему уравнений имеют аналитические выражения:

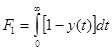
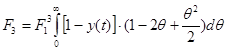
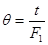, θ – измененный масштаб по времени

Обычно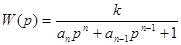

Последовательность расчета коэффициентов моделей:

1. Разбивается ось абсцисс исходной кривой разгона на отрезки времени с интервалом Δt из условия, что на протяжении графика в пределах 2Δt исходная кривая мало отличается от прямой.

2. Значения y в конце каждого интервала Δt делят на y(∞) и получают нормированное значение переходной функции.

t	Y	1-y	θ	1-θ	(1-y)* (1-θ)
Δt	y(Δt)	1-y(Δt)	Δt/F1
2Δt	y(2Δt)	1-y(2Δt)	2Δt/F1
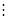
nΔt	y(nΔt)	1-y(nΔt)	nΔt/F1

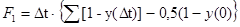
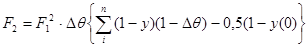
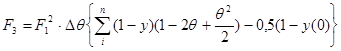
Методика идентификации моделей объектов III-го порядка по их временным характеристикам

Данный метод выгодно отличается своей простотой и оперативностью. При той же точности решения вычислительные затраты на обработку кривой разгона снижаются, по сравнению с известным методом М.П. Симою. При этом круг рассматриваемых объектов значительно расширяется.

Типы моделей

Модель объекта определяется в виде дифференциального уравнения. Причем вид уравнения зависит от вида кривой разгона.

Уравнение объекта берётся в виде:

3. a₃y^'''+a₂y^''+a₁y^'+y=x, (1)

если кривые разгона объекта имеют вид:

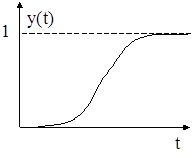
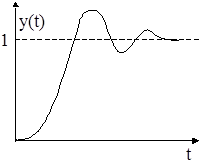
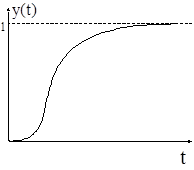
4. a₃y^'''+a₂y^''+a₁y^'+y=b₁x^'+x, (2)

если кривые разгона объекта имеют вид:

5. a₃y^'''+a₂y^''+a₁y^'+y=b₁x^', (3)

если кривая разгона объекта имеет вид:

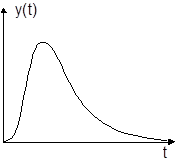
Дата добавления: 2015-10-24