Оценивание весовой функции по методу наименьших квадратов

Рассмотрим систему с одним входом и одним выходом. Объект предполагается линейным и стационарным.

Выход системы запишем в виде:

(1)

h(t) - весовая функция (импульсная переходная функция)

x(t-t)- вход, n(t) - невязка (иногда называют шумом),

TS - время установления, определяется как min интервал времени, измеренный от момента подачи импульсного сигнала до момента, когда реакция системы составит 5% пикового значения (рис.). Входная и выходная переменные представлены в формуле (1) в виде отклонений от своих математических ожиданий, т.е.

Представим уравнение (1) в дискретном виде

или (2)

Здесь - время установления, - время измерения выхода, N_i - содержит не только невязку в моменты времени n(iD), но и ошибки аппроксимации функции x(t-t).

В результате аппроксимации задача оценивания непрерывной функции h(t) заменяется (параметризуется) оцениванием конечного множества параметров h₀ ,..., h_Ns-1 (называется дискретной импульсной переходной функцией)

Для упрощения представления запишем уравнения (2) в матричном виде:

(3)

Запишем матричное представление в символическом виде

(4)

Задача сводится к определению вектора параметров b при заданной матрице А и вектора измерений z.

Критерием при оценивании вектора параметров b является выбор таких b, которые минимизируют сумму квадратов невязок на интервале измерений.

Положим в матричном виде J = n^T n (5)

подставляя (4) в (5) получим J=(z-Ab)^T (z-Ab)

Необходимо определить b^*, удовлетворяющие условию

.

Необходимым условием вычисления J является выполнение условия экстремума .

Запишем уравнения (3) в виде сумм

(6)

Продифференцируем (6) J по компонентам вектора b:

=

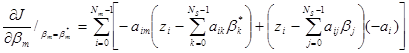= -2 при m = 0,1,..., N_S –1 (7)

Формулу (7) представим в матричном виде:

(8)

(8) является необходимым условием экстремума J.

Достаточным условием при расчете min J является положительная определенность квадратной матрицы

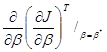
Если формулу (8) продифференцируем еще раз по b, то получим

(9)

Если матрица A^TA - неособенная, и также правая часть не зависит от b в (9), то условие экстремума (8) является необходимым и достаточным условием минимума.

Перепишем (8) в виде:

A^TA b* = A^Tz, отсюда b* = (A^TA)^-1 A^Tz (10)

Напомним, что

.

В непрерывной форме уравнение (10) принимает вид

(11)

Уравнение (11) – уравнение Винера-Хопфа и может быть переписано в виде

где R_xx(t) - автокорреляционная функция и R_xz(t) - взаимная корреляционная функция.

Автокорреляционной функцией случайного процесса X(t) называется неслучайная функция двух аргументов K_xx(t,t‘), которая при каждой паре значений t,t‘ равна корреляционному моменту соответствующему случайному сечению функции X(t).

K_xx(t,t‘) = .

Дата добавления: 2015-10-24