Характеристик объектов управления

Рассматривается объект с одним входом и одним выходом со свойствами: стационарности, линейности, сосредоточенности параметров. На вход подается ступенчатое воздействие и на выходе снимается кривая разгона. Необходимо решить обратную задачу: по известной кривой разгона определить коэффициенты уравнения.

Для представления уравнений в безразмерной форме выполняется математическая обработка кривой разгона. Пересчитывается ордината кривой разгона (операция тарирования) по формуле , где - экстремальные значения выходной величины.

При описании динамических свойств статических промышленных объектов ограничиваются одним из следующих дифференциальных уравнений

T₁, T₂, T₃ - коэффициенты левой части дифференциального уравнения;

T - коэффициент при первой производной в правой части дифференциального уравнения;

R_{0 -} коэффициент усиления объекта.

В уравнении 3-го порядка могут быть T₃, T₂, t = 0, тогда получаем частные случаи уравнений 1-го и 2-го порядков, и без запаздывания.

Для описания динамических свойств астатических объектов используются дифференциальные уравнения не содержащие члена y(t) и статического коэффициента усиления k₀, т.е. имеющих вид:

.

Величина запаздывания t может быть определена графически следующим образом (см. рис).

2. Идентификация параметров модели апериодического звена 1-го порядка по временным характеристикам

Для апериодического звена 1-го порядка

коэффициент усиления k₀ определяется следующим образом

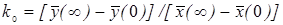
Для апериодического звена первого порядка:

- передаточная функция

- переходная функция;

- импульсная переходная функция.

Реакция на единичное входное воздействие

Для определения коэффициента звена:

Временные характеристики.

Если зависимость экспоненциальная, то постоянная времени определяется одним из двух способов. При первом, чисто графическом способе проводится касательная в любой точке графика и берётся разность абсцисс точек: а) касания с графиком и б) пересечения с линией установившегося уровня. При втором способе необязательно производить графические построения. Рассмотрим момент времени t=T: 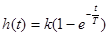, тогда h(T)≈0,63k.

С соответствующими корректировками те же способы применимы и при наличии импульсной переходной характеристики. Для второго метода при t=T: , тогда ω(T)≈0,37k.

Если переходная характеристика имеет вид:

,то нужно в передаточную функцию вводить чистое запаздывание:

Дата добавления: 2015-10-24