
Читайте также:
|
ВСТУП
Проектування сучасних автоматичних систем керування в нафтовій і газовій промисловості вимагає від інженера глибокого знання в області моделювання технологічних процесів, як об’єктів керування.
Задачі побудови математичної моделі керованого об’єкта, синтез систем керування і її аналіз, оцінка якості керування входять в етап проектування автоматичних систем керування.
Мета курсової роботи це складання і дослідження математичних моделей деяких типових об’єктів автоматизації.
В сучасні методи синтезу замкнутих систем керування входять, як правило, відомості про динамічні характеристики керованих об’єктів. Для аналізу і синтезу усієї замкнутої системи керування вихідним матеріалом служить математичний опис керованого об’єкта. Якщо такий опис невідомий, то теорія не може дати правильної відповіді на питання, які виникають в процесі проектування автоматичної системи керування.
Математичну модель керованого об’єкта можна визначити двома способами. Можна або ідентифікувати систему за результатами експерименту або шукати необхідний математичний опис розрахунковим шляхом, використовуючи загальні фізичні закони, відомості про конструкцію і технологічні параметри обладнання.
Кожен із методів має свої переваги і недоліки. Експериментальний метод можна реалізувати лише тоді, коли система, що досліджується уже побудувалася. При правильно поставленому експерименті можна одержати необхідну інформацію про поведінку системи, досліджуючи вже відомі промислові об’єкти. Але при цьому неможливо одержати повну уяву про внутрішню структуру системи і вказати як динамічні характеристики можуть впливати на вибір найкращої конструкції.
ЗАВДАННЯ НА КУРСОВУ РОБОТУ (ВАРІАНТ 37)

Рисунок 1.1 – Схема гідравлічного об’єкта
Таблиця 1.1 - Вихідні дані для курсової роботи
| Варіант | Геометричні розміри ємності, м | Тиски, МПа | Витрати, кг/с | Номінальні значення Н1 і Н2, м | ||||||||
| L1 | D1 | L2 | D2 | P0(1) | P0(2) | P1 | P2 | Q1(0) | Q2(0) | H1(0) | H1(0) | |
| 2.0 | 1.0 | 1.5 | 0.9 | - | - | - | - | 0.6 | 1.6 |
СТВОРЕННЯ МАТЕМАТИЧНОЇ МОДЕЛІ
ОБ’ЄКТА
Математична модель – це система математичних співвідношень, які описують досліджуваний процес або явище. В основу методу покладено ідентичність форми рівнянь і однозначність співвідношень між змінними в рівняннях оригіналу і моделі, тобто, їхню аналогію.
Даний об’єкт являється гідравлічним. В ньому протікають процеси, які описуються законом матеріального балансу.
Для складання математичної моделі керованого об’єкта приймаємо наступні допущення:
- ємності 1 і 2 мають постійний поперечний переріз S=const;
- газ, який знаходиться над рідиною є ідеальним і його температура не зміниться;
- коефіцієнт місцевого опору є сталим.
Рівняння матеріального балансу для керованого об’єкту має наступний вигляд:
(швидкість накопичення рідини) = (притік) – (витік) (1.1)
Задачею регулювання є стабілізація рівня Н1 і Н2, яка здійснюється за допомогою клапанів і шляхом зміни витрати Q3.
Структурна схема даного гідравлічного об’єкта має вигляд, показаний на рис.1.2.

Рисунок 1.2 – Структурна схема керованого об’єкта
Складаємо рівняння матеріального балансу для ємності 1. Швидкість накопичення рідини - це зміна об’єму в часі. Отже, маємо наступне:
 (1.2)
(1.2)
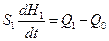 (1.3)
(1.3)
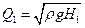 (1.4)
(1.4)
 (1.5)
(1.5)
З врахуванням (1.3) - (1.5) можна записати:
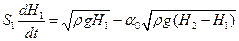 (1.6)
(1.6)
де S1 – поперечний переріз ємності 1, м;
H1, H2 – рівні рідини в ємностях 1 і 2 відповідно;
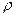 - густина рідини, кг/м3;
- густина рідини, кг/м3;
g – прискорення вільного падіння, м2/с;
Q0, Q1, Q2 – витрати рідини в ємностях і трубі;
 ,
,  - коефіцієнт місцевого опору труби;
- коефіцієнт місцевого опору труби;
Формула (1.6) є математичною моделлю для ємності 1.
Тепер складаємо рівнянн матеріального балансу для ємності 2:
 (1.7)
(1.7)
 (1.8)
(1.8)
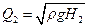 (1.9)
(1.9)
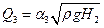 (1.10)
(1.10)
З врахуванням (1.7) – (1.10) можна записати:
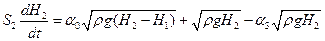 (1.11)
(1.11)
де S2 – поперечний переріз ємності 2;
 ,
,  - коефіцієнт місцевого опору труби;
- коефіцієнт місцевого опору труби;
Таким чином, матимемо наступну формулу:
 (1.12)
(1.12)
Рівняння (1.12) і буде математичною моделлю даного керованого об’єкту.
ЛІНЕАРИЗАЦІЯ МАТЕМАТИЧНОЇ МОДЕЛІ ОБ’ЄКТА
Лінеаризація – це процес переходу від нелінійних диференціальних рівнянь до лінійних. Процес лінеаризації нелінійного рівняння виконується шляхом розкладання нелінійних функцій, що входять в це рівняння в ряд Тейлора. Лінеаризація буде правильною, якщо відхилення вхідної величини від рівноважного стану буде невеликим, отже величинами, що мають порядок вище першого можна знехтувати.
Запишемо модель, яку потрібно лінеаризувати:
 (2.1)
(2.1)
Нехай:

Отже, проводимо лінеаризацію системи рівнянь (2.1):
 (2.2)
(2.2)
 (2.3)
(2.3)
Рівняння рівноваги для керованого об’єкта мають наступний вигляд:
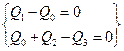 (2.4)
(2.4)
Підставивши в цю систему отримані раніше дані, можна записати:
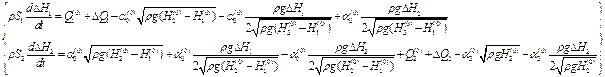 (2.5)
(2.5)
Введемо наступні заміни:

Приведемо лінеаризовану математичну модель до форми Коші, яка для нашого випадку матиме наступний вигляд:
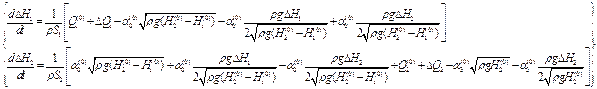 (2.6)
(2.6)
Подамо математичну модель у формі Коші:
 (2.7)
(2.7)
Тепер виведемо формули для обчилення коефіцієнтів aij та bij:
 (2.8)
(2.8)
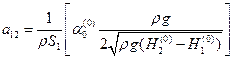 (2.9)
(2.9)
 (2.10)
(2.10)
 (2.11)
(2.11)
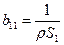 (2.12)
(2.12)
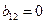 (2.13)
(2.13)
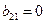 (2.14)
(2.14)
 (2.15)
(2.15)
Напишемо формули для обчислення коефіцієнтів місцевих опорів  і
і  , виходячи з рівностей (1.7) - (1.10):
, виходячи з рівностей (1.7) - (1.10):
 (2.16)
(2.16)
 (2.17)
(2.17)
Проводимо необхідні обчислення (Додаток А) та отримуємо потрібні нам значення:
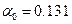
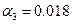
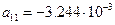


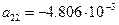
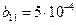
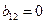
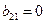

Після обчислень значень коефіцієнтів отримуємо:
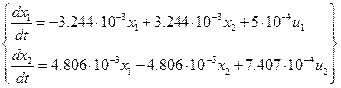 (2.18)
(2.18)
Таким чином, рівняння (2.18) утворюють математичну модель лінеаризованого керованого об’єкта.
Дата добавления: 2015-10-24; просмотров: 196 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Регрессионный метод идентификации линейных систем (Метод наименьших квадратов) | | | ПОШУК МАТРИЧНОЇ ПЕРЕДАВАЛЬНОЇ ФУНКЦІЇ ОБ’ЄКТА |