Пошук матричної передавальної функції об’єкта

Матриця W(p), елементи передавальної функції W_ij(p) i-го виходу відносно j-го входу, називається матричною передавальною функцією. Матричні передавальні функції у випадку багатозв’язних систем знайшли широке використання в інженерній практиці. Це пояснюється двома причинами: по-перше, матричні передавальні функції дають можливість оперувати з алгебраїчними, а не диференціальними рівняннями, по-друге, матрична передавальна функція дозволяє зменшити розмірність задачі.

Матриця W(p) для нашого керованого об'єкта має розмірність 2х2, при двох входах і двох змінних стану об'єкта.

Нехай КО описується системою лінійних диференціальних рівнянь:

(3.1)

Систему рівнянь (3.1) перетворимо за Лапласом при нульових початкових умовах:

(3.2)

Матрична передавальна функція для КО має вигляд:

(3.3)

Як приклад, визначимо 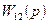. Прирівнюємо до нуля і одержуємо систему рівнянь

(3.4)

з якої визначаємо:

(3.5)

або

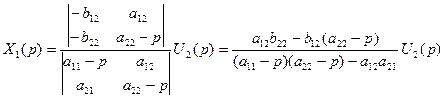(3.6)

Отже,

(3.7)

Аналогічно можуть бути знайдені інші передавальні функції . Знаючи , математичну модель запишемо у такій формі:

(3.8)

де

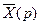- матриця-стовпець з елементами , ,

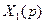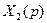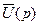- матриця-стовпець з елементами , .

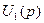Тепер перейдемо до обчислення матричної передавальної функції керованого об'єкта.

Нехай керований об'єкт описується системою лінійних диференціальних рівнянь:

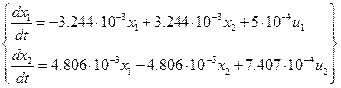(3.9)

Систему рівнянь (3.9) перетворимо за Лапласом при нульових початкових умовах:

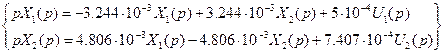(3.10)

(3.11)

Прирівнюємо до нуля і одержуємо систему рівнянь:

(3.12)

З системи рівнянь (3.12) одержуємо:

(3.13)

Отже,

(3.14)

Аналогічно знаходимо і інші передавальні функції W_ij(p).

(3.15)

(3.16)

Повертаємось до системи (3.11) і прирівнюємо до нуля 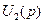. Одержуємо наступну систему рівнянь:

(3.17)

З системи рівнянь (3.8) одержуємо:

(3.18)

(3.19)

(3.20)

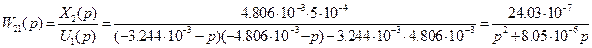(3.21)

В результаті отримуємо матричну передавальну функцію керованого об’єкта, яка має наступний вигляд:

(3.22)

Передавальна функція керованого об’єкта, представлена виразом (3.21), повністю характеризуватиме динамічні властивості керованого об’єкта, який описується системою рівнянь (3.9). Знаючи W(p), математичну модель керованого об’єкта запишемо в такій формі:

(3.23)

Рівняння (3.23) - це спрощена форма математичної моделі керованого об’єкта. Вона має дві складові, а саме матрицю W(p), знайдену раніше, та матрицю U(p), елементи якої взяті з системи початкових диференційних рівнянь (3.9).

Дата добавления: 2015-10-24