Метод передавальної матричної функції

Для дослідження математичної моделі даним методом нам потрібно подати нашу математичну модель у вигляді матричної передавальної функції, яка має вигляд:

(4.22)

де (4.23)

х_і(р) - зображення по Лапласу і-тої передавальної величини;

U_j(p) - зображення по Лапласу j-тої передавальної величини.

Для знаходження матричної передавальної функції виконаємо пряме перетворення Лапласа.

(4.24)

або

(4.25)

Приймаємо значення u₂(p)=0 і знаходимо х₁(р) і х₂(р), використавши правило Крамера для розв'язку системи:

(4.26)

Отже, в результаті отримаємо наступні вирази:

(4.27)

(4.28)

Тепер приймаємо U₁(p)=0 і знаходимо х₁(р) і х₂(р) таким самим способом як і вище:

(4.29)

(4.30)

Далі знаходимо значення елементів передавальної матричної функції. (4.31)

(4.32)

(4.33)

(4.34)

(4.35)

(4.36)

(4.37)

(4.38)

Таким чином, провівши ряд обчислень отримали значення елементів матричної передавальної функції. Проведемо узагальнення, тобто запишемо матричну передавальну функцію в остаточному вигляді. Вона буде мати наступний вигляд.

(4.39)

(4.40)

Тепер можемо приступити до дослідження математичної моделі керованого об'єкта. Загальна формула для проведення дослідження має наступний вигляд:

(4.41)

u(p) - зображення по Лапласу вхідних сигналів.

На вхід об'єкта подаються сигнали:

(4.42)

Зображення по Лапласу цих величин матиме такий вигляд:

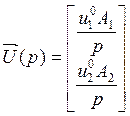(4.43)

Отже, зображення по Лапласу вихідних величин виглядає так:

(4.39)

Після нескладних обрахунків в результаті отримали наступне значення:

(4.44)

Тепер потрібно зробити зворотнє перетворення Лапласа з отриманих зображень вихідної величини. Зворотнє перетворення Лапласа робимо за теоремої лишки, тобто:

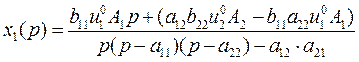(4.45)

(4.46)

Для одержання застосовуємо зворотне перетворення Лапласа. , обчислення оригінала вихідних величин зручно проводити за допомогою теореми лишків.

Розглянемо рівняння (4.20) та (4.21) і згідно теореми лишків матимемо:

(4.47)

де n-кількість полюсів.

Знайдемо зміну вихідної величини X₁(t) i X₂(t). Для цього скористаємося зворотнім перетворенням Лапласа виразів (4.20) та (4.21).

Всі подальші обчислення методу матрично-передавальної функції проведені в середовищі ПП Mathсad і занесені в Додаток Б.

В результаті дослідження я отримав графіки перехідних характеристик рівнів H1 і H2 (рис.4.2).

Рисунок 4.2 – Результат дослідження методом матрично-передавальної

функції

Дата добавления: 2015-10-24