Загальне поняття економетричної моделі

При аналізі економічних явищ на основі економіко-математичних методів особливе місце займають моделі, що виявляють кількісні зв’язки між показниками, що вивчаються, і чинниками, що впливають на них. Науковою дисципліною, предмет якої складає вивчення цієї кількісної сторони економічних явищ і процесів засобами математичного і статистичного аналізу, є економетрія, в якій результати теоретичного аналізу економіки синтезуються з висновками математики і статистики. Основне завдання економетрії - перевірка економічних теорій на фактичному (емпіричному) матеріалі за допомогою методів математичної статистики.

Головним інструментом економетрії служить економетрична модель, тобто економіко-математична модель факторного аналізу, параметри якої оцінюються засобами математичної статистики. Ця модель виступає засобом аналізу і прогнозування конкретних економічних процесів на основі реальної статистичної інформації.

Економічна модель – це спрощене уявлення про економічну дійсність чи її фрагмент, позбавлене різних деталей та подробиць, несуттєвих в даному відношенні для розуміння головних властивостей та взаємозв’язків в досліджуваному явищі. Моделі можуть бути вербальними, графічними, аналітичними. Графічні та аналітичні моделі (в силу їх наочності та виразності) суттєво підвищують можливості теоретичного моделювання.

В будь якій моделі в явному чи неявному вигляді містяться певні припущення і передумови. В моделях використовуються два типа економічних змінних: екзогенні та ендогенні. Значення екзогенних змінних вводяться з зовні і задаються до початку роботи моделі – це вихідна інформація. З аналізу моделі роблять певні висновки про властивості зображеної моделлю економічної дійсності. Так формуються значення ендогенних змінних. Вони є результатом моделювання. В результаті побудови моделі ми отримуємо описання того, як екзогенні змінні впливають на ендогенні. Отриманні в результаті аналізу моделі висновки можуть бути підтверджені чи спростовані виходячи з фактів, що спостерігаються в дійсності. На цій основі модель визнається такою, що відповідає дійсності або потребує корекції.

Звичайно, кожна модель відображає економічну дійсність лише певною мірою. Тому при перевірці її відповідності реальності важливо, щоб ті характеристики економічної дійсності, які не знайшли відображення в моделі або не аналізуються в даний момент, не змінювалися, інакше результати можуть виявитися далекими від висновків, отриманих за допомогою моделі. Ця умова виражається за допомогою припущення «за інших рівних умов».

Математична модель об’єкта містить у собі три групи елементів: 1) характеристику об’єкта, яку потрібно визначити (невідомі величини), – вектор ; 2) характеристики зовнішніх (щодо модельованого об’єкта) умов, які змінюються, – вектор ; 3) сукупність внутрішніх параметрів об’єкта – .

Множини умов та параметрів 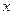та можуть розглядатись як екзогенні величини, а величини, що належать вектору , – як ендогенні.

Математичну модель можна тлумачити як особливий перетворювач зовнішніх умов об’єкта 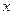на характеристики об’єкта , які мають бути знайдені.

Залежно від способу вираження співвідношень між зовнішніми умовами, внутрішніми параметрами та характеристиками, які мають бути знайдені, математичні моделі поділяються на дві групи: структурні та функціональні.

Структурні моделі відбивають внутрішню організацію об’єкта: його складові частини, внутрішні параметри, їх зв’язок з 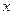та . Основна ідея функціональних моделей – пізнання сутності об’єкта через найважливіші прояви цієї сутності: діяльність, функціонування, поведінку. Внутрішня структура об’єкта при цьому не вивчається, а тому інформація про структуру не використовується. Функціональна модель описує поводження об’єкта так, що задаючи значення 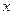, можна дістати значення :

Побудувати функціональну модель – означає знайти оператор , який пов’язує 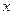та .

Відмінності між структурними та функціональними моделями мають відносний характер. Вивчення структурних моделей дає одночасно цінну інформацію про поводження об’єкта. З іншого боку, при вивченні функціональних моделей необхідно сформулювати гіпотези про внутрішню структуру об’єкта.

Економетрична модель – це функція чи система функцій, що описує кореляційно – регресійний зв’язок між економічними показниками, один чи кілька з яких є залежною змінною, інші – незалежними.

Економетричні моделі належать до функціональних математичних моделей. Вони кількісно описують зв’язок між вхідними показниками економічної системи – 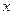та результативними показниками – . У загальному вигляді економетричну модель можна записати так: 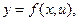де 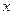– вхідні економічні показники, – випадкова чи стохастична складова.

В попередніх гіпотезах завжди має місце така фактична ситуація: результативна змінна частково визначається невідомими факторами, які ми не можемо врахувати в моделі. Такі фактори є випадковими, і необхідно оцінити їх випадковий вплив. Для цього потрібно змінити модель, ввівши до неї випадкову складову .

Показники 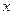найчастіше бувають детермінованими. Адитивна складова є випадковою змінною, а отже, з огляду на те, що залежна змінна і від неї залежить, вона також є стохастичною. Звідси випливає висновок: економетрична модель є стохастичною.

Економетрична модель може являти собою як дуже складну систему, так і просту формулу. В будь-якому випадку вона потребує знань з економіки та статистики. Спочатку для визначення відповідних взаємозв’язків використовують знання економіки, а потім для оцінки кількісної природи взаємозв’язків, отримані за попередні періоди данні обробляються за допомогою статистичних методів.

Це статичні моделі. Деякі інвестиційні організації використовують широкомасштабні економетричні моделі, щоб на основі прогнозів таких факторів, як бюджет, очікувані споживчі витрати і планові інвестиції в ділову сферу, робити прогнози відносно майбутнього рівня ВВП, інфляції, безробіття. Інші фірми і некомерційні організації спеціалізуються на таких моделях, продаючи інвестиційним інститутам, фінансистам корпорацій, суспільним агентам і ін. або прогнози, або комп’ютерні програми. Широкомасштабні моделі такого типу нараховують велику кількість рівнянь, які описують багато важливих взаємозв’язків. Не дивлячись на те, що оцінки таких взаємозв’язків ґрунтуються на даних за минулий період, ці оцінки можуть дозволити моделі ефективно працювати в майбутньому.

Коли прогнози виявляються невірними, іноді кажуть, що взаємозв’язок, що лежить в основі моделі зазнав структурних зрушень. Невдача може бути наслідком впливу неврахованих в моделі факторів. Та і інша ситуація вимагають зміни або величини оцінок, або самої концепції економетричної моделі, або того і іншого. Рідко можна зустріти користувача, який би не змінював таку модель час від часу по мірі накопичення досвіду.

Економетричні моделі можна класифікувати за рядом класифікаційних ознак.

За аналітичною формою моделі (рівняння) виділяють лінійні, нелінійні, степеневі моделі, моделі Брандона та ін.

Наприклад, модель Брандона має вигляд: , де – показник (результативні ознаки), що вивчається; 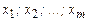– величини (факторні ознаки), що впливають на .

Якщо користуватися терміном «змінна», то у будь-якій досить складній економічній системі можна виділити внутрішні змінні (випуск продукції, чисельність працівників, виробіток) і зовнішні змінні (обсяг постачання ресурсів, кліматичні умови та ін.). Тоді, за напрямом і складністю зв’язків між внутрішніми (ендогенними, вихідними) і зовнішніми (екзогенними, вхідними) змінними виділяють наступні економетричні моделі: регресійні моделі, взаємозалежні системи, рекурсивні системи.

Регресійними називають моделі, засновані на рівнянні регресії або системі регресійних рівнянь, що позв’язують величини ендогенних і екзогенних змінних. Розрізняють моделі парної і множинної регресії.

Для знаходження параметрів регресійних моделей використовуються частіше метод найменших квадратів (МНК).

Взаємозалежні системи якнайповніше описують економічну систему, що містить, як правило, множину взаємозв’язаних ендогенних і екзогенних змінних. Такі моделі задаються системою взаємозалежних рівнянь виду ( – число ендогенних змінних, – число екзогенних змінних):

Для знаходження параметрів системи взаємозалежних рівнянь використовуються складніші методи: двох- і трьох- крокові МНК, методи максимальної правдоподібності з повною і неповною інформацією та ін.

На практиці прагнуть спростити взаємозалежні системи і привести їх до так званого рекурсивного виду. Для цього спочатку вибирають ендогенну змінну (внутрішній показник), залежну тільки від екзогенних змінних (зовнішніх чинників), – . Потім вибирається внутрішній показник, який залежить тільки від зовнішніх чинників і від і т.д.; таким чином, кожен наступний показник залежить тільки від зовнішніх чинників і від внутрішніх попередніх. Такі системи називаються рекурсивними. Параметри першого рівняння рекурсивних систем знаходять МНК, їх підставляють в друге рівняння і знову застосовується МНК, і т.д.

Процес побудови і використання економетричних моделей є досить складним і включає наступні основні етапи:

– визначення мети дослідження, побудова системи показників і логічний відбір чинників, що найбільше впливають на кожен показник;

– вибір форми зв’язку показників, що вивчаються, між собою і відібраними чинниками, іншими словами, вибір типу економетричної моделі;

– збір початкових даних і аналіз інформації;

– побудова економетричної моделі, тобто визначення її параметрів;

– перевірка якості побудованої моделі, в першу чергу її адекватності економічному процесу, що вивчається;

– використання моделі для економічного аналізу і прогнозування.

При практичній реалізації вказаних етапів дуже важливою є побудова системи показників досліджуваного економічного процесу і визначення переліку чинників, що впливають на кожен показник.

Вкажемо основні вимоги, що пред’являються до чинників економетричної моделі:

– кожен чинник має бути обґрунтований теоретично;

– в перелік доцільно включати тільки найважливіші чинники, які істотно впливають на показники, що вивчаються; при цьому рекомендується, щоб кількість чинників, що включаються в модель, не перевищувала однієї третини від числа спостережень у вибірці (довжини часового ряду);

– чинники мають бути лінійно не залежними, оскільки ця залежність означає, що вони характеризують аналогічні властивості досліджуваного явища. Наприклад, заробітна плата працівників залежить, разом з іншими чинниками, від росту продуктивності праці і від обсягу продукції, що випускається. Проте ці чинники можуть бути тісно взаємозв’язані, корельовані і, отже, в модель доцільно включати тільки один з них. Включення в модель лінійно взаємозалежних чинників призводить до виникнення явища мультиколінеарності, яке негативно позначається на якості моделі;

– чинники, що впливають на економічний процес, можуть бути кількісні і якісні. До моделі рекомендується включати тільки такі чинники, які можуть бути чисельно виміряні;

– в одну модель не можна включати сукупний чинник і одиничні чинники, з яких він формується. Одночасне включення таких чинників призводить до невиправдано збільшеного їх впливу на залежний показник, до спотворення реальної дійсності.

При відборі чинників використовуються статистичні методи відбору. Так, істотного скорочення числа чинників можна досягти за допомогою покрокових процедур відбору змінних. Жодна з цих процедур не гарантує отримання оптимального набору змінних. Проте при практичному застосуванні вони дозволяють отримувати досить хороші набори істотно впливаючих чинників, крім того їх можна поєднувати з іншими підходами до вирішення цієї задачі, наприклад, з експертними оцінками значимості чинників. Серед покрокових процедур відбору чинників найчастіше використовуються процедури покрокового включення і виключення чинників. Обидві ці процедури добре формалізовані і тому успішно реалізовані в різних машинних програмах статистичного аналізу.

Метод виключення припускає побудову рівняння, що включає усю сукупність змінних, з подальшим послідовним (покроковим) скороченням числа змінних в моделі до тих пір, поки не досягається виконання деякої наперед заданої умови. Суть методу включення - в послідовному включенні змінних в модель до тих пір, поки регресійна модель не відповідатиме заздалегідь встановленому критерію якості. Послідовність включення визначається за допомогою частинних коефіцієнтів кореляції: змінні, що мають відносно досліджуваного показника більше значення частинного коефіцієнта кореляції, першими включаються в регресійне рівняння.

Дата добавления: 2015-10-23