Прогнозування за багатофакторною регресійною моделлю

Якщо побудована модель виявилася адекватною, то ми можемо використовувати її для знаходження прогнозних значень результативної змінної.

Припустимо, нам відомі значення факторів в період , тоді ми можемо отримати прогнозне значення за моделлю:

Інтервальні прогнози результативної змінної з рівнем довіри для побудованої моделі обчислюються за формулами:

для індивідуального значення залежної змінної:

для математичного сподівання:

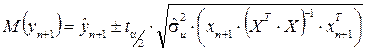
Приклад 3. Багатофакторна лінійна регресія

Для десяти цехів машинобудівного підприємства наведено такі дані (табл. 5.1). Побудувати багатофакторну лінійну регресію, яка описуватиме зв’язок продуктивності праці з наведеними чинниками.

Таблиця 5.1. Вихідні дані задачі

Номер цеху	Продуктивність праці, тис. грн.	Середньомісячна зарплата, грн.	Фондомісткість продукції, тис. грн.	Виконання норми виробітку , %
			0,20
			0,04
			0,30
			0,20
			0,10
			0,10
			0,25
			0,03
			0,15
			0,32

Розв’язання

Продуктивність праці залежить від трьох чинників – середньомісячної зарплати, фондомісткості продукції та відсотку виконання норми виробітку. Загальний вигляд трифакторної регресійної лінійної моделі буде такий:

,

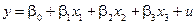де – продуктивність праці, тис. грн.; – середньомісячної зарплата, грн., – фондомісткість продукції, тис. грн., – відсоток виконання норми виробітку; – стохастична складова, – параметри моделі, а вибіркової регресійної моделі:

,

де – оцінки параметрів моделі.

Щоб мати явний вигляд залежності, необхі­дно знайти (оцінити) невідомі параметри за МНК.

Введемо допоміжну змінну 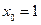, яка відповідатиме параметру і запишемо модель в матричному вигляді: . Тоді оцінки параметрів можна знайти за формулою:

;

;

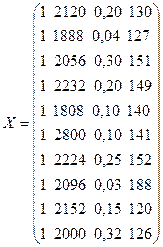
Виконавши необхідні розрахунки, отримуємо:

В результаті модель має вигляд:

Виконаємо перевірку статистичної значимості оцінок параметрів моделі за допомогою t -критерію Стьюдента. Для цього виконаємо необхідні розрахунки:

; ; ;

; ; ;

Коли стандартні помилки параметрів більші за абсолютні значення оцінок цих параметрів, то це може означати, що оцінка параметра є зміщеною. Якщо, наприклад, стандартна помилка на 10 % перевищує абсолютне значення оцінки параметра, то можна говорити про те, що цей параметр має зміщення щодо його істинного значення. Така ситуація спостерігається стосовно оцінки 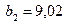і її стандартної помилки 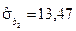: або .

Критичне значення критерію Ст’юдента для рівня значимості та ступенів вільності ( – кількість параметрів) знаходимо за допомогою таблиць 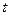–розподілу Ст’юдента: .

Оскільки, < , то оцінка вважається статистично значимою, тобто, зі ймовірністю 95% вплив рівня середньомісячної зарплати на продуктивність праці визнається істотним. > , > , > , тому оцінки зі ймовірністю 95% не є статистично значимими, що підтверджує нульову гіпотезу про неістот­ність впливу змінних та на результативну ознаку .

Довірчі межі коефіцієнтів регресії зі ймовірністю 0,95:

або

аб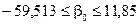о

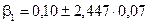або

або

Коефіцієнт детермінації використовується як критерій щільності зв’язку між залежною та незалежними змінними:

З цього випливає, що варіація залежної змінної на 86% визначається варіацією незалежних змінних.

З урахуванням кількості чинників та кількості спостережень обчислимо скоригований коефіцієнт детермінації:

Виконаємо перевірку моделі на адекватність за – критерієм Фішера.

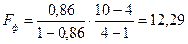
Задаємо рівень значимості: .

За статистичними таблицями – розподілу Фішера з ступенями вільності та заданим рівнем значимості знаходимо критичне значення критерію: . 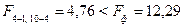, то зі ймовірністю 0,95 ми стверджуємо, що побудована нами модель є адекватною.

Оскільки побудована модель виявилася адекватною, то ми можемо використовувати її для знаходження прогнозних значень результативної змінної.

Припустимо, нам відомі значення чинників в період – , тоді ми можемо отримати прогнозне значення :

Інтервальні прогнози результативної змінної з рівнем довіри для побудованої моделі:

для індивідуального значення:

;

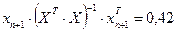
для математичного сподівання:

Дата добавления: 2015-10-23