Приклад 4. Побудова економетричної моделі на основі покрокової регресії

Для десяти цехів машинобудівного підприємства наведено такі дані (табл. 5.1). Побудуємо економетричну модель, яка описуватиме зв’язок продуктивності праці з наведеними чинниками згідно з алгоритмом покрокової регресії.

Розв’язання

Крок 1-й. Усі вихідні дані стандартизуються (нормалізуються) (табл. 5.2.)

Таблиця 5.2. Розрахункові дані задачі

Показники
Сума			1,69
Середнє значення	52,3	2137,6	0,169	142,4
Стандартне відхилення	8,25	255,72	0,10	18,60

Таблиця 5.3. Значення стандартизованих показників

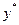
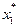
-0,885	-0,069	0,319	-0,667
-1,249	-0,976	-1,328	-0,828
-0,279	-0,319	1,349	0,462
0,327	0,369	0,319	0,355
-1,491	-1,289	-0,711	-0,129
2,146	2,590	-0,711	-0,075
0,449	0,338	0,834	0,516
0,570	-0,163	-1,431	2,452
0,327	0,056	-0,196	-1,205
0,085	-0,538	1,555	-0,882

Крок 2-й.Запишемо кореляційну матрицю для вихідних даних:

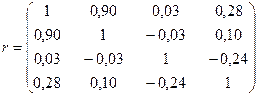
З матриці очевидно, що діагональні її елементи дорівнюють одиниці, бо вони характеризують зв’язок кожної змінної із собою. Ця матриця квадратна і симетрична.

У першому рядку містяться коефіцієнти парної кореляції, що характеризують тісноту зв’язку кожної змінної з продуктивністю праці.

Так, 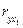= 0,9; 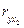= 0,03; 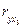= 0,28, де – продуктивність праці; – зарплата; – фондомісткість продукції; – відсоток виконання норми виробітку.

Крок 3-й. Оскільки серед величин максимальне значення 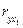= 0,9, то спочатку побудуємо модель: .

,

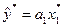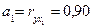Крок 4-й. Порівнявши два інші коефіцієнти: max{ 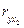= 0,03; 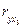= 0,28} = 0,28, введемо до моделі змінну : 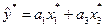і, нарешті,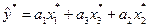

Для моделі 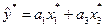система нормальних рівнянь запишеться так:

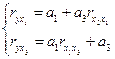
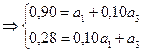
Для моделі 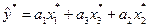система нормальних рівнянь запишеться так:

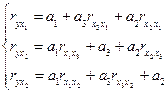
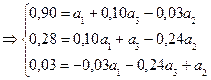
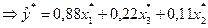
Далі, використовуючи співвідношення 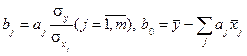, обчислимо оцінки параметрів моделі для вихідної нестандартизованої інформації:

У результаті дістанемо такі регресійні рівняння зв’язку:

;

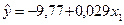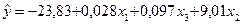
Приклад 5. Оцінка коефіцієнтів детермінації

Порівняємо коефіцієнти детермінації для різних економетричних моделей, побудованих для вихідних даних, наведених у табл. 5.1, на основі покрокової регресії.

Таблиця 5.4. Коефіцієнти детермінації

Економетрична модель		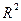з урахуванням числа ступенів свободи
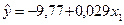
	0,810	0,787
	0,847	0,757
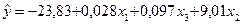
	0,858	0,716

З табл. 5.4. бачимо, що з додатковим введенням нової незалежної змінної коефіцієнти детермінації 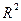без урахування числа ступенів свободи збільшуються, з урахуванням числа ступенів свободи 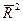– зменшуються, для першої моделі, в яку включається всього одна незалежна змінна, 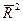має найбільше значення, а для третьої – з трьома незалежними змінними – найменше. Тобто для третьої моделі в результаті введення додаткової змінної зменшення величини 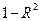не зможе компенсувати збільшення відношення 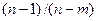. Зауважимо при цьому, що коефіцієнти детермінації без урахування числа ступенів свободи мають більші числові значення, ніж з урахуванням цього числа.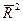

Приклад 6. Перевірка адекватності моделі

Обчислимо F-критерій для економетричних моделей, розглянутих у прикладі 4 (табл. 5.5).

Таблиця 5.5. Перевірка адекватності моделі

Економетрична модель		Число ступенів свободи		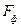Знак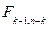
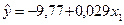
	0,05		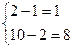34,24	>
	0,05		77,78	>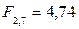
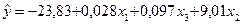
	0,05		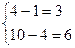108,82	>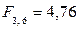

Отже, відповідні економетричні моделі є достовірними, тобто підтверджується гіпотеза про те, що кількісна оцінка зв’язку між залежною і незалежними змінними в моделях є істотною.

Дата добавления: 2015-10-23