Основні припущення в багатофакторному регресійному аналізі

Багатофакторна лінійна регресійна модель є уза­гальненням простої лінійної регресійної моделі, тому всі основні класичні припущення для неї зберігають­ся, але дещо модифікуються.

1. Математичне сподівання залишків дорівнює нулю.

2. Значення 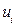вектора залишків 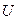незалежні між собою, тобто відсутня серійна кореляція.

3. Модель гомоскедастична.

4. Коваріація між випадковою величиною 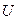та кож­ною незалежною змінною 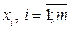дорівнює 0.

Відзначимо, що властивість 4 виконується автоматично, якщо 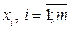не стохастичні та припу­щення 1 має силу.

5. Модель повинна бути правильно специфікованою.

6. Випадкова величина 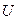підпорядковується нормаль­ному закону розподілу з нульовим математичним сподіванням і постійною дисперсією.

7. Відсутність мультиколінеарності між факторами 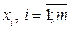, тобто фактори повинні бути незалежними один від одного. Не повинно бути точного лінійного зв’язку між двома або більше факторами.

Припущення 7 для простої лінійної регресії від­сутнє, але надзвичайно важливе для багатофакторної регресії.

Якщо всі припущення класичної лінійної регресій­ної моделі виконуються, то МНК-оцінки є не тільки лінійними без відхилень оцінками, але мають ще най­меншу дисперсію, тобто є BLUE -оцінками.

Етапи побудови багатофакторної регресійної моделі

Процес побудови багатофакторної регресійної моделі більш складний, ніж простої; він складається з багатьох досить кропітких етапів.

Можна виділити такі етапи побудови багатофак­торної регресійної моделі:

1. Вибір та аналіз усіх можливих факторів, які впливають на процес (або показник), що вивчається.

2. Вимірювання та аналіз знайдених факторів.

3. Математико-статистичний аналіз факторів.

4. Вимір методу та побудова регресійної багато­факторної моделі.

5. Оцінка невідомих параметрів.

6. Перевірка моделі на адекватність.

7. Розрахунок основних характеристик та побу­дова інтервалів довіри.

8. Аналіз отриманих результатів, висновки.

Дата добавления: 2015-10-23