Приклад 2. Нелінійна парна регресія

На основі статистичних даних показника і фактора знайти оцінки параметрів лінії регресії, якщо припустити, що стохастична залежність між ними має вигляд:

Оцінити щільність зв’язку на основі коефіцієнта детермінації. Використовуючи критерій Фішера з надійністю , оцінити адекватність побудованої моделі статистичним даним.

Якщо прийнята математична модель адекватна, то з тією ж надійністю знайти довірчу область базисних даних.

Побудувати графіки фактичних даних, лінії регресії та довірчу область базисних даних.

Таблиця 4.1. Вихідні дані задачі

	1,10	1,55	2,09	2,52	3,07	3,57	4,05	4,56	5,06	5,53
	2,08	6,06	11,65	19,10	29,29	40,10	54,00	70,65	87,53	125,63

Розв’язання

Розглянемо модель виду:

Відповідна вибіркова модель матиме вигляд:

Степенева модель є нелінійною за факторами та параметрами. Для оцінки її параметрів використаємо МНК, але спочатку модель потрібно привести до лінійного виду. Для цього про логарифмуємо праву та ліву частину рівняння:

Нехай,

Тоді,

Ми отримали лінійну модель, що і дає змогу розраховувати оцінки параметрів МНК.

При цьому як вихідну інформацію будемо використовувати значеннями та .

. Лінійна модель матиме вигляд: .

Оскільки , то .

Отже, досліджуваний зв’язок виражатиметься моделлю, що має вигляд:

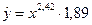
Знайдемо розрахункові значення (дані розрахунків в табл. 4.2.).

Таблиця 4.2. Розрахункові дані задачі

	2,08	1,10	0,73	0,10	0,07	0,01	0,87	2,38	1783,46	1808,72
	6,06	1,55	1,80	0,44	0,79	0,19	1,70	5,45	1533,51	1486,03
	11,65	2,09	2,46	0,74	1,81	0,54	2,42	11,22	1114,49	1086,30
	19,10	2,52	2,95	0,92	2,73	0,85	2,87	17,65	727,00	650,71
	29,29	3,07	3,38	1,12	3,79	1,26	3,35	28,44	261,40	234,67
	40,10	3,57	3,69	1,27	4,70	1,62	3,71	40,96	13,29	20,33
	54,00	4,05	3,99	1,40	5,58	1,96	4,02	55,57	120,19	88,19
	70,65	4,56	4,26	1,52	6,46	2,30	4,30	74,03	865,53	678,13
	87,53	5,06	4,47	1,62	7,25	2,63	4,56	95,20	2559,84	1842,21
	125,63	5,53	4,83	1,71	8,27	2,92	4,77	118,01	5387,86	6564,40
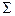
	446,09	–	–	-	41,44	14,29	–	–	14366,59	14459,69

Оцінимо щільність зв’язку між залежною змінною та незалежною – , тобто визначимо, наскільки значимим є вплив змінної на .

Коефіцієнт детермінації:

Постільки значення коефіцієнта детермінації близьке до 1, то можна вважати, що побудована модель є адекватною і варіація пояснюється переважно варіацією .

Перевірка моделі на адекватність за –критерієм Фішера:

Розраховуємо величину –критерію:

Задаємо рівень значимості, наприклад, . На цьому етапі за статистичними таблицями –розподілу Фішера з ступенями вільності критичне значення .

Оскільки, , то зі ймовірністю 0,95 ми стверджуємо, що побудована нами модель є адекватною.

Щоб знайти довірчу область базисних даних, за формулами, приведеними в пункті 3.10. знаходимо межі інтервальних прогнозів для лінійної регресії, а потім шляхом зворотних перетворень (потенціювання) меж довірчих інтервалів прогнозу для лінійної регресії знайдемо межі надійних інтервалів для побудованої моделі 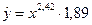. Розрахунки представлені в табл. 4.3.

Таблиця 4.3. Розрахункові дані

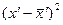
	0,73	0,10	0,87	0,0179	0,98	0,23	0,64	1,09	1,90	2,98
	1,80	0,44	1,70	0,0113	0,42	0,21	1,49	1,90	4,42	6,72
	2,46	0,74	2,42	0,0014	0,12	0,20	2,22	2,62	9,20	13,70
	2,95	0,92	2,87	0,0063	0,03	0,20	2,67	3,07	14,50	21,47
	3,38	1,12	3,35	0,0009	0,00	0,20	3,15	3,54	23,39	34,58
	3,69	1,27	3,71	0,0005	0,04	0,20	3,52	3,91	33,65	49,86
	3,99	1,40	4,02	0,0008	0,10	0,20	3,82	4,22	45,56	67,79
	4,26	1,52	4,30	0,0022	0,19	0,20	4,10	4,51	60,50	90,58
	4,47	1,62	4,56	0,0071	0,29	0,21	4,35	4,76	77,55	116,88
	4,83	1,71	4,77	0,0039	0,39	0,21	4,56	4,98	95,80	145,38
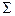
	32,56	10,84	–	0,0522	2,54	–	–	–	–	–

Для лінійної моделі .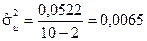

Нехай, рівень значимості , тоді з 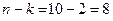ступенями вільності .

Похибку прогнозу обчислюємо за формулою:

Довірчі зони для 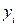знайдемо за формулою:

Графіки фактичних даних, лінії регресії та довірча область базисних даних представлені на рис. 4.1.

Рис. 4.1. Нелінійна парна регресія залежності від та довірча область базисних даних

Дата добавления: 2015-10-23