Бінарна логістична регресія

Лінійна регресія

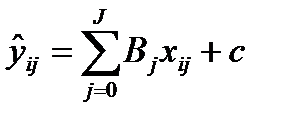
Дозволяє розрахувати усереднені значення на ґрунті прямолінійного узагальнення.

Діаграма розподілу чистих значень (виміряні %% розподіли для відповіді “Так”) та усереднених значень на ґрунті прямолінійного узагальнення.

Логістична регресія (бінарна, порядкова, мультиноміальна)

Логістична регресія (бінарна, порядкова, мультиноміальна) встановює зв’язок між певним(ми) чистим(ми) значенням(ми) факторної(них) змінної(них) x_i; x_ij та очікуваними (латентними) значеннями показникової змінної y* з використанням логарифмічної функції.

Діаграма розподілу чистих значень (виміряні %% розподіли для відповіді “Так”), усереднених значень на ґрунті прямолінійного узагальнення та усереднених значень на ґрунті криволінійного (логістичного) узагальнення.

Будь-яке криволінійне моделювання є точнішим за прямолінійне – сума квадратів відхилень чистих значень від лінії узагальнених значень завжди є меншим при криволінійному моделюванні, аніж при прямолінійному.

Отже, з точки зору евристичного потенціалу логістична регресія має батаго переваг над лінійною регресією.

Показникова та логарифмічна функції

Показникова функція: y=a^x (a>0, a≠1)

Логарифмічна функція: y=log_ax (a>0, a≠1)

Логарифмічна та показникова функції є взаємно оберненими.

Графіки показникової і логарифмічної функцій з однаковою основою (a) є симетричними відносно прямої y=x.

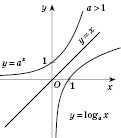
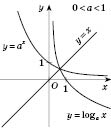
Рис. 1 Рис. 2

Якщо основа логарифмічної функції дорівнює 10 (а=10), тоді обчислюється десятковий логарифм

y=log₁₀x=lg x

Відповідна показникова функція: y=10^x

Якщо основою логарифмічної функції є число e (ірраціональне число (константа Ейлера), яка дорівнює приблизно 2,718281…), тоді обчислюється натуральний логарифм

y=log_ex=ln x

Зворотна (показникова) функція до натурального логарифма – експонентна функція (експонента (exp)).

Відповідна показникова функція: y=exp(x)=e^x

БІНАРНА ЛОГІСТИЧНА РЕГРЕСІЯ

Бінарна логістична регресія встановлює зв’язок між фактором/рами, який/які виміряний/ні неперервними шкалами (порядковими, інтервальними, метричними) та показниковою дихотомною змінною.

У випадку з дихотомною показниковою змінною йдеться про певну подію, яка може або відбутись, або не відбутись.

Якщо подія відбулась, то дихотомна показникова змінна має код 1.

Якщо подія не відбулась, то дихотомна показникова змінна має код 0.

Пригадаймо, що у такий спосіб в SPSS базі даних ми кодуємо відповіді, проміряні багатоваріантними номінальними шкалами.

В рамках бінарної логістичної регресії в контексті передбачування очікуваного (латентного) значення показникової змінної (y*) використовується такий статистичний показник, як:

ймовірність того, що досліджувана подія відбудеться.

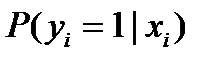
Іншим важливим статистичним показником бінарної логістичної регресії є:

Odds ratio

Дата добавления: 2015-10-24