Нелінійні моделі та їх лінеаризація

Найбільш популярною моделлю в економіці є лінійна регресія. Проте не всі економічні процеси можна нею моделювати. Тому на практиці використовуються складніші моделі з нелінійною залежністю між показником та факторами .

За методикою оцінки параметрів нелінійні регресії розглядаються двох видів: 1) нелінійні за факторами, але лінійні за невідомими параметрами, які підлягають оцінці; 2) нелінійні за факторами і параметрами.

Регресії, нелінійні за факторами, але лінійні за оцінюваними параметрами, називаються квазілінійними.

Парну квазілінійну регресію можна записати в загальному вигляді:

Заміною величин нелінійна парна регресія приводиться до лінійної парної регресії: . Тоді для оцінки параметрів використовується МНК і формули набувають вигляду:

, .

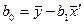Квазілінійну модель з більше ніж одним фактором в загальному вигляді можна записати так:

Якщо, , то .

Приклад.

Гіпербола

Нехай,

Тоді,

Щільністьі нелінійного зв’язку вимірюють з допомогою коефіцієнта детермінації (див. п. 3.8.)

Для оцінки адекватності нелінійних моделей спостережуваним даним можна використовувати критерій Фішера. Перевірка виконується за таким же алгоритмом, що й для лінійної парної регресії (див. п. 3.9.).

Довірчі межі прогнозу для квазілінійної парної регресії оцінюються за тими ж формулами, що й для лінійної парної регресії, лише замість розглядають (див. п. 3.10.).

В регресіях нелінійних за факторами та параметрами логарифмують праву та ліву частину рівняння і проводять заміну змінних. Таким чином нелінійна регресія зводиться до лінійного виду. Це дає змогу для оцінки параметрів використовувати МНК.

Приклад.

Степенева функція

Про логарифмують праву та ліву частину рівняння:

Нехай,

Тоді,

Показникова функція

Про логарифмують праву та ліву частину рівняння:

Нехай,

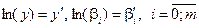
Тоді,

Параметри лінійної моделі оцінюють за відомими формулами, використовуючи в якості вихідних даних значення нових змінних – та , якщо потрібно.

Параметри нелінійної моделі 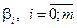знаходять з рівнянь:

.

У тих випадках, коли нелінійна регресія перетворюється в лінійну шляхом логарифмування і заміни змінних, інтервальний прогноз знаходять для відповідної лінійної регресії, а потім, використовуючи зворотні перетворення до меж інтервалів довіри прогнозу лінійної регресії, знаходять межі інтервалів довіри прогнозу нелінійної регресії.

Розглянемо показникову парну регресію:

Для приведення цієї регресії до лінійної, потрібно прологарифмувати праву та ліву частини моделі і зробити заміну змінних:

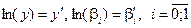
За формулами, приведеними в пункті 3.10. знаходимо межі інтервальних прогнозів для лінійної регресії, а потім шляхом зворотних перетворень (потенціювання) меж довірчих інтервалів прогнозу для лінійної регресії знаходять межі надійних інтервалів показникової регресії:

Дата добавления: 2015-10-23