Побудова кореляційних функцій та спектральних густин об’єкта

Для математичного опису випадкових сигналів використовують поняття випадкового процесу, який можна визначити як сімейство випадкових змінних 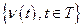, які залежать від параметра t. Цей параметр може приймати як дискретні значення, так і бути неперервним. В першому випадку , де Z множина цілих чисел і , h – період (час) квантування. Якщо t неперервна величина, то або .

Якщо Т – множина дискретних значень , то випадковий процес називається процесом з дискретним часом. У тому випадку, коли t – неперервна величина, то маємо процес з неперервним часом.

В процесі спостереження за системою завжди отримують певну функцію часу , яка називається реалізацією процесу або вибірковою функцією.

Серед усіх типів випадкових процесів у теорії керування особливе місце займають стаціонарні випадкові процеси.

Випадкові процеси 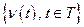називаються стаціонарними, якщо розподіл , , 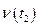…, тотожно дорівнює розподілу , ,…, для всіх значень . Якщо рівні тільки перші і другі моменти розподілу (математичне сподівання і дисперсія), то процес носить назву слабо стаціонарного.

Важливими характеристиками стаціонарного процесу є математичне сподівання та дисперсія.

Із визначення стаціонарного процесу випливає, що розподіл густини ймовірності однаковий для всіх значень t і може бути записане як , тобто стаціонарний процес має постійне математичне сподівання

(6.1)

і постійну дисперсію

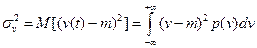. (6.2)

Якщо спостереження за випадковим процесом ведуться у дискретні моменти часу , то

(6.3)

і

. (6.4)

При реалізації випадкового процесу завжди мають справу з кінцевим проміжним часу спостережень, тому за формулами (8.4) і (8.5) отримують не точні значення величин m і , а їх оцінки і .

Математичне сподівання і дисперсія випадкового процесу є точковими його характеристиками і мають зміст середнього значення та відхилення відносно m.

Для характеристики структури випадкового стаціонарного процесу використовують коваряційні функції

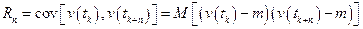. (6.5)

Нормоване значення носить назву автокореляційної функції випадкового процесу

. (6.6)

Для n =0 із формули (8.6) випливає, що , тому .

Нехай для значень 0, 1, 2, …, за формулою (8.7) обчислені величини 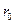, ,…, , тоді можна утворити матрицю

, (6.7)

Матриця (6.7) називається автокореляційною матрицею.

Для стаціонарного випадкового процесу матриця симетрична і додатно визначена. Додатна визначеність матриці означає, що визначник і всі головні мінори матриці додатні.

Із формули (6.6) випливає, що автокореляційна функція безрозмірна. Так як , то знання автокореляційної функції еквівалентно знанню коваріаційної функції і навпаки.

Формула (6.6) дає можливість визначити автокореляційну функцію стаціонарного випадкового процесу , який спостерігається нескінченно довго. На практиці завжди маємо справу з кінцевою часовою послідовністю , ,…, за якою можна знайти тільки оцінки автокореляцій.

(6.8)

де

, (6.9)

n =0,1,…,s – оцінка автоковаріації.

Для отримання змістовної оцінки автокореляції N повинно бути не менше 50, а .

Якщо відома коваріаційна функція

, (6.10)

де - часовий зсув; то у відповідність до неї можна поставити функцію спектральної щільності

. (6.11)

Задача знаходження коваріаційної функції (6.11) є двоякою задачею, оскільки за відомим значенням можна знайти

. (6.12)

Функція спектральної щільності є характеристикою розподілу потужності і дисперсії сигналу за частотою.

Програма для побудови кореляційних функцій і спектральних густин виконана в середовищі ПП Matlab і наведена в Додатку Г. Результати досліджень, а саме автокореляційна функція вхідного і вихідного сигналів, взаємокореляційна функція, спектральна густина вхідного і вихідного сигналів наведені нижче (рис.6.1 - 6.24).

Рисунок 6.1 – Графік формування вхідного і вихідного сигналу для W11

Рисунок 6.2 – Автокореляційна функція вхідного сигналу для W11

Рисунок 6.3 – Взаємокореляційна функція сигналу для W11

Рисунок 6.4 – Автокореляційна функція вихідного сигналу для W11

Рисунок 6.5 – Спектральна густина вхідного сигналу для W11

Рисунок 6.6 – Спектральна густина вихідного сигналу для W11

Рисунок 6.7 – Графік формування вхідного і вихідного сигналу для W12

Рисунок 6.8 – Автокореляційна функція вхідного сигналу для W12

Рисунок 6.9 – Взаємокореляційна функція сигналу для W12

Рисунок 6.10 – Автокореляційна функція вихідного сигналу для W12

Рисунок 6.11 – Спектральна густина вхідного сигналу для W12

Рисунок 6.12 – Спектральна густина вихідного сигналу для W12

Рисунок 6.13 – Графік формування вхідного і вихідного сигналу для W21

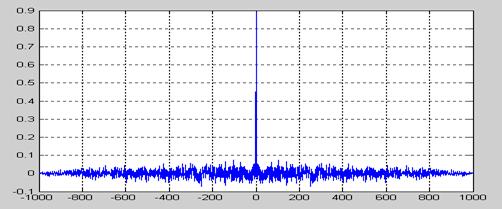
Рисунок 6.14 – Автокореляційна функція вхідного сигналу для W21

Рисунок 6.15 – Взаємокореляційна функція сигналу для W21

Рисунок 6.16 – Автокореляційна функція вихідного сигналу для W21

Рисунок 6.17 – Спектральна густина вхідного сигналу для W21

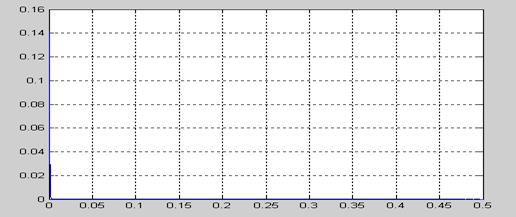
Рисунок 6.18 – Спектральна густина вихідного сигналу для W21

Рисунок 6.19 – Графік формування вхідного і вихідного сигналу для W22

Рисунок 6.20 – Автокореляційна функція вхідного сигналу для W22

Рисунок 6.21 – Взаємокореляційна функція сигналу для W22

Рисунок 6.22 – Автокореляційна функція вихідного сигналу для W22

Рисунок 6.23 – Спектральна густина вхідного сигналу для W22

Рисунок 6.24 – Спектральна густина вихідного сигналу для W22

Одним з результатів побудови кореляційної функції та спектральної густини є отримання матриць значень математичного сподівання та середнього квадратичного відхилення для для досліджуваного КО (рис.6.25).

Рисунок 6.25 – Матриці значень математичного сподівання та середнього квадратичного відхилення для для досліджуваного КО

ВИСНОВОК

Під час розробки курсової роботи мені довелося зіткнутись з такими завданнями, як складання математичної моделі, розрахунок її параметрів, лінеаризація, а також обчислення лінеарезованої моделі за допомогою аналітичних і числових методів.

В результаті проведення обчислень за допомогою сучасної обчислювальної техніки та програмного забезпечення Mathcad і MatLab на основі дослідних даних ми можемо сказати що під впливом масових витрат, керуючої дії регулюючого пристрою рівні рідини в першій і другій посудинах змінюються на деякому проміжку часу.

Під час знаходження розв’язку лінеаризованої математичної моделі аналітичними і числовим методами ми, скориставшись даними параметрів гідравлічного об’єкта, які були нами обчислені в попередніх пунктах, отримали графік залежності зміни рівня рідини в посудинах від часу з якого випливає, що отримані результати аналітичного і числового методів практично співпадають.

В останніх двох розділах я виконав побудову часових і частотних характеристих, а також кореляційної функції, спектральної густини та їх числових даних для досліджуваного КО.

Дата добавления: 2015-10-24