Інтегрування ірраціональних функцій

Інтеграл від будь-якої раціональної функції, як було показано вище, завжди виражається в скінченному вигляді, чого не можна сказати про інтеграл від функції ірраціональної. Однак можна вказати на деякі підкласи ірраціональних функцій, інтеграли від яких виражаються у скінченному вигляді.

Загальний спосіб, за допомогою якого вдається знайти інтеграл від ірраціональної функції, полягає в тому, що внаслідок тієї чи іншої підстановки інтеграл від ірраціональної функції зводиться до інтеграла від функції раціональної. Тому цей спосіб називають раціоналізацією заданого інтеграла.

Розглянемо підкласи ірраціональних функцій, інтеграли від яких виражаються в скінченному вигляді.

1. Інтеграл вигляду

де R - раціональна функція, m_i i n_i > 1- натуральні числа (і= 1, 2,…, р).

Цей інтеграл раціоналізується за допомогою підстановки х=t^k, де к - найменший спільний знаменник дробів (i= 1, 2, …, p).

2. Інтеграл вигляду

де R - раціональна функція, m_i i n_i > 1- натуральні числа (і= 1, 2,…, р) і визначник 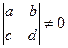(a, b, c, d - сталі дійсні числа).

Цей інтеграл раціоналізується за допомогою підстановки

де к - найменший спільний знаменник дробів (і= 1, 2,…, р).

3. Інтеграл вигляду

Цей інтеграл зводиться до табличного шляхом виділення повного квадрата із квадратного тричлена.

4. Інтеграл вигляду

Для знаходження цього інтеграла спочатку виділяємо в чисельнику похідну квадратного тричлена ах²+вх+с, після чого розкладаємо інтеграл на суму двох інтегралів:

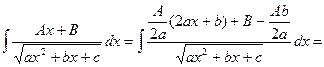
Перший із одержаних інтегралів є табличний інтеграл (4), а другий розглянутий в п.3.

5. Інтеграл вигляду

Підстановкою зводять цей інтеграл до розглянутого в п. 3.

6. Інтеграл вигляду

де m, n i p - раціональні числа, 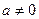i називають інтегралом від диференціального бінома. Цей інтеграл виражається в скінченному вигляді у таких трьох випадках:

1) р - ціле число;

2) ціле число;

3) ціле число,

причому в усіх трьох випадках ціле число може бути додатним, від`ємним, або дорівнювати нулю.

Перший випадок: р - ціле число. Підстановка

x=t^k,

де к - найменший спільний знаменник дробів m i n, раціоналізує інтеграл.

Другий випадок: ціле число.

У цьому випадку інтеграл раціоналізується підстановкою

a+bxⁿ=t^s,

де s - знаменник числа р.

Третій випадок: ціле число.

У цьому випадку для раціоналізації інтеграла застосовують підстановку

де s- знаменник числа р.

7. Інтеграл вигляду де R - раціональна функція.

Шляхом виділення повного квадрата із квадратного тричлена ax ²+ bx + c цей інтеграл зводиться до одного із трьох інтегралів:

1)

2)

3)

Ці інтеграли знаходять відповідно за допомогою підстановок

1) z=m sin t;

2) z=m tg t;

3)

Дата добавления: 2015-10-30