Розв´язання прикладів

Приклад 1. Знайти

Розв`язання. Скориставшись властивостями 4 і 5 невизначеного інтеграла, будемо мати

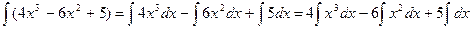
Далі застосувавши до перших двох одержаних інтегралів формулу (3), а до третього- властивість 3 (формула 2), остаточно знаходимо

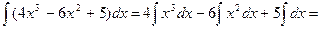
де

Відзначимо, що додавати довільну сталу після знаходження кожного інтеграла, як це зроблено в даному прикладі, не слід. Досить всі довільні сталі підсумувати і результат, позначений однією буквою C, записати вкінці, тобто після того, як всі інтеграли будуть знайдені.

Приклад 2. Знайти

Розв`язання. Помічаємо, що

Тоді

= .

Приклад 3. Знайти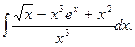

Розв`язання. Маємо

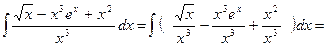
Приклад 4. Знайти .

Розв`язання. Виконуючи тотожні перетворення підінтегральної функціїї, будемо мати

.

Тому

.

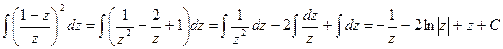Приклад 5. Знайти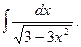

Розв`язання. Маємо

Приклад 6. Знайти .

Розв`язання. Оскільки 1 + cos2 x= 2cos² x, то

Приклад 7. Знайти .

Розв`язання. Відомо, що

Тому

Приклад 8. Знайти

Розв`язання. Виконуємо тотожні перетворення над підінтегральною функцією:

Отже,

Приклад 9. Знайти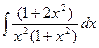

Розв`язання. Враховуючи, що 2 x ² =x ² +x ², будемо мати

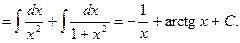
Приклад 10. Знайти

Розв`язання. В силу табличного інтеграла (3) з урахуванням, що u= tg x, одержимо

Приклад 11. Знайти

Розв`язання. Тут підносити двочлен до 19-го степеня недоцільно, так як u= 5 x+ 3-лінійна функція. Виходячи із табличного інтеграла

і формули (23), згідно з якою

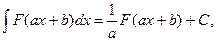
одержимо

Приклад 12. Знайти

Роз`вязання. Так як

і 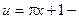лінійна функція, то в силу формули (23), будемо мати

Приклад 13. Знайти

Розв`язання. Маємо

Так як то в якості змінної інтегрування маємо вираз 7-cos²x. Відносно цієї змінної одержимо інтеграл від степеневої функції, тобто

Розв`язання даного прикладу можна записати ще й так:

Проведені міркування можна записати і інакше, а саме:

Приклад 15. Знайти

Розв`язання. Оскільки похідна виразу 5+7tg x дорівнює , а множник відрізняється від цієї похідної лише сталим множником 7, то змінною інтегрування тут можна вважати вираз 5+7tg x і таким чином, знайти інтеграл за формулою (6):

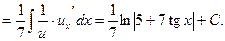
Приклад 16. Знайти

Розв`язання. Заданий інтеграл можна податити у вигляді:

але і тому, вважаючи змінною інтегрування функцію arctg 2 x, інтеграл беремо за формулою (8):

Приклад 17. Знайти .

Розв`язання.

ВПРАВИ

Знайти інтеграли:

1. 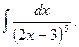Відповідь: .

2. Відповідь: .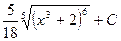

3. Відповідь: .

4. Відповідь: .

5. Відповідь: .

6. Відповідь: .

7. 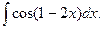Відповідь: .

8. Відповідь: C- cos e^x.

9. Відповідь: .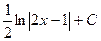

10. Відповідь: .

11. Відповідь: .

12. Відповідь: .

13. 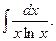Відповідь: .

14. Відповідь: .

15. Відповідь: .

16. Відповідь: .

17. 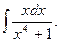Відповідь: .

18. Відповідь: .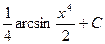

19. Відповідь: .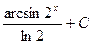

20. Відповідь: .

21. Відповідь: e^x+e^-x+C.

22. Відповідь: .

23. Відповідь: .

24. Відповідь: .

25. 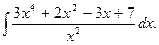Відповідь: .

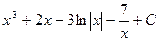26. .

Відповідь: .

27. Відповідь: .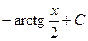

28. 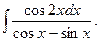Відповідь: .

29. 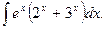Відповідь: .

30. Відповідь: .

1.5. Інтегрування методом заміни змінної (метод підстановки)

Метод заміни змінної застосовують в тих випадках, коли безпосередньо (за допомогою таблиці) не вдається знайти первісну.

При розв`язанні прикладів заміна змінної здійснюється за допомогою підстановок двох видів:

1) 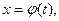де - монотонна, неперервно диференційовна функція нової змінної t.

В цьому випадку формула заміни змінної набуває вигляду

(24)

2) де u - нова змінна.

Формула заміни змінної при такій підстановці має вигляд

(24а)

Передбачається, що після інтегрування буде здійснюватись знову перехід до початкової змінної х.

Відзначимо, що загального правила, яке указувало б, яку підстановку треба вибрати, не існує. Однак для багатьох видів інтегралів підстановка відома і буде розглянута нами далі.

Зауважимо також, що уміння вибрати підстановку так, щоб знаходження інтеграла спростилось, досягається розв`язанням великої кількості вправ.

Дата добавления: 2015-10-30