Розв`язання прикладів. Приклад 1. Обчислити

Приклад 1. Обчислити

Розв`язання. Функції u=x і v=-e^-x неперервні разом із своїми похідними і на відрізку , отже за формулою (33)

Приклад 2. Обчислити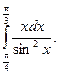

Розв`язання. Покладемо u=x, 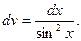Тоді du=dx, Оскільки u=x, v=- ctg x, i неперервні на відрізку , то в силу формули (33)

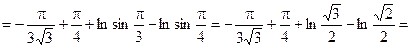
Приклад 3. Обчислити

Розв`язання. Враховуючи, що u= ln(x+ 1), dv=dx за формулою (33), одержимо

Приклад 4. Обчислити

Розв`язання. Застосовуючи двічі формулу інтегрування частинами, будемо мати

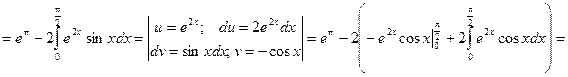
Розв`язуючи далі одержане рівняння відносно шуканого інтеграла, знаходимо

Звідси остаточно одержимо

Приклад 5. Обчислити

Розв`язання. Згідно з формулою інтегрування частинами

Вправи

Обчислити інтеграли:

1. Відповідь:

2. Відповідь:

3. Відповідь: 6-2 e.

4. Відповідь:

5. Відповідь:

6. Відповідь:

7. Відповідь:

8. Відповідь:

9. Відповідь:

10. Відповідь:

2.6. Обчислення визначених інтегралів, яке грунтується на властивостях підінтегральної функції

1. Якщо f (x) непарна функція, тобто f (-x)= -f (x), то

.

2. Якщо f (x) парна функція, тобто f (-x)= f (x), то

3.Якщо функція f(x) періодична з періодом Т, тобто f (x+T) =f (x), то

де n – ціле число.

Розв`язання прикладів

Приклад 1. Обчислити

Розв`язання. Оскільки функція непарна, бо

а відрізок інтегрування – симетричний, то відразу робимо висновок, що заданий інтеграл дорівнює нулю.

Приклад 2. Обчислити

Розв`язання. Підінтегральна функція парна, так як Тому

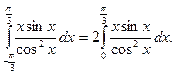
Беручи інтеграл за формулою інтегрування частинами, одержимо

Таким чином, шуканий інтеграл

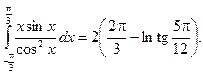
Приклад 3. Обчислити

Розв`язання. Подаючи даний інтеграл у вигляді суми двох інтегралів і враховуючи, що під знаком першого інтеграла функція непарна, а під знаком другого – парна, будемо мати

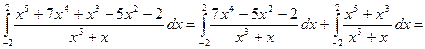
Приклад 4. Обчислити

Розв`язання. Підінтегральна функція є періодичною функцією з періодом , бо

Тому можна від верхньої і нижньої меж інтегрування відняти число . Тоді

Вправи

1. Обчислити Відповідь: 0.

2. Обчислити 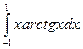Відповідь:

3. Обчислити Відповідь: 0

4. Обчислити Відповідь:

5. Обчислити

Відповідь:

6. Розглянемо інтеграл Легко зробити висновок, що він дорівнює 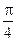. Дійсно,

З іншого боку, зробивши підстановку одержимо

Цей результат явно неправильний, так як підінтегральна функція а це означає, що визначений інтеграл від такої функції не може дорівнювати від`ємному числу (див. властивість 7). В чому помилка?

Відповідь: підстановка не придатна, бо ця функція розривна при t= 0.

7. Обчислити Відповідь: 1.

8.Чому дорівнюють інтеграли:

a) 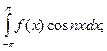б)

якщо: а) f (x) – парна функція; б) f (x) – непарна функція?

Відповідь:

а) Якщо f (x) – парна функція, то

a

б). Якщо f (x) – непарна функція, то

a

Питання для самоперевірки

1. Дайте означення визначеного інтеграла.

2. Сформулюйте теорему існування визначеного інтеграла.

3. Сформулюйте і доведіть властивості визначеного інтеграла.

4. Що називають середнім значенням функції f(x) на відрізку ?

5. Чому дорівнює похідна від визначеного інтеграла із змінною верхньою межею інтегрування?

6. Сформулювати і вивести формулу Ньютона –Лейбніца.

7. В чому суть методів заміни змінної (підстановки) і інтегрування частинами у визначеному інтегралі?

8. Вивести спрощену формулу для визначеного інтеграла, взятого по симетричному відрізку від парної і непарної функцій.

Вправи

Обчислити інтеграли:

1. Відповідь:

2. 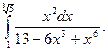Відповідь:

3. Відповідь:

4. Відповідь: 3,5.

5. Відповідь: ln1,5.

6. 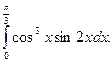Відповідь:

7. Відповідь:

8. Відповідь:

9. Відповідь: 0.

10. Відповідь:

11. Відповідь:

12. Відповідь: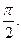

13. 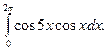Відповідь: 0.

14. Відповідь:

15. Відповідь:

16. 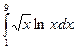Відповідь:

17. Відповідь:

18. Відповідь:

19. Відповідь: 0.

20. Відповідь:

21. Відповідь: 1,5(0,5+ln1,5).

22. Чи можна в інтегралі зробити підстановку .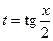

Зробивши підстановку будемо мати

Результат явно неправильний, так як підінтегральна функція додатна, і тому інтеграл від цієї функції не може дорівнювати нулю. В чому помилка?

Відповідь: підстановка 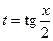не придатна, бо ця функція розривна при

23. Чи можна в інтегралі зробити підстановку ?

Відповідь: неможна, так як а відрізок інтегрування .

3. Невласні інтеграли

Невласними інтегралами називають інтеграли з нескінченними проміжками інтегрування (інтеграли з нескінченними межами інтегрування) і інтеграли від необмежених функцій (інтеграли від функцій, які мають нескінченний розрив).

2.7. Невласні інтеграли з нескінченними проміжками інтегрування

Нехай функція f (x) визначена на проміжку 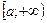і інтегровна на відрізку при всякому b>а. Тоді визначений інтеграл існує при всякому і, отже, він є деякою функцією від b, визначеною на проміжку , тобто

Якщо функція I (b)при має скінченну границю А, то цю границю називають невласним інтегралом від функції f (x)на проміжку 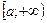і позначають

Таким чином, за означенням

(34)

При цьому вважають, що невласний інтеграл збігається (до числа А).

Якщо ж функція при не має скінченної границі, то у цьому разі вважають, що невласний інтеграл 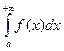розбігається.

Аналогічно визначається невласний інтеграл вигляду

Коли функція f (x) визначена в проміжку і інтегровна на відрізку при всякому а<b, то за означенням

(35)

Невласний інтеграл називають збіжним, якщо існує скінченна границя, що стоїть у правій частині рівності (35) і розбіжним, якщо такої скінченної границі не існує.

Нарешті, якщо функція f (x) визначена на проміжку то за означенням,

(36)

де с – яке-небудь стале число, причому невласний інтеграл називають збіжним, якщо збігаються обидва невласних інтеграли, які стоять у правій частині рівності (36). Якщо ж принаймні один з цих інтегралів розбігається, то невласний інтеграл називають розбіжним.

2.8. Ознаки збіжності невласних інтегралів з нескінченними проміжками інтегрування

1. Якщо f (x) і –дві невід`ємні функції на проміжку 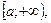інтегровні на відрізку при всякому b>a і якщо для то із збіжності невласного інтеграла випливає збіжність невласного інтеграла а із розбіжності невласного інтеграла 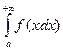випливає розбіжність невласного інтеграла

2. Якщо при

,

причому c> 0, і 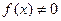для всіх достатньо великих х, то невласні інтеграли i або обидва збігаються, або обидва розбігаються.

3. Якщо збігається то збігається і де с – величина стала.

4. Якщо функція f(x) визначена на проміжку і інтегровна на відрізку при всякому b>а, то із збіжності невласного інтеграла випливає збіжність і невласного інтеграла причому

Зауважимо, що невласний інтеграл називають абсолютно збіжним, якщо збігається інтеграл .

Якщо ж невласний інтеграл збігається, а інтеграл розбігається, то невласний інтеграл називають умовно збіжним.

5. Нехай функція f (x) невід`ємна на проміжку (a> 0) і інтегровна на відрізку при всякому b>a. Якщо

для

де с – константа, а число то невласний інтеграл збігається.

Якщо ж

для

де с –константа, а число то невласний інтеграл розбігається.

2.9. Заміна змінної у невласному інтегралі

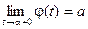Нехай функція f (x) визначена і неперервна при Якщо функція , яка визначена на проміжку ( і можуть бути і нескінченними), має неперервну похідну і , , то

Дата добавления: 2015-10-30