Розв`язання прикладів. Приклад 1. Знайти

Приклад 1. Знайти

Розв`язання. Маємо інтеграл вигляду де m= 5, n= 4.

Враховуючи, що m=5 >0 i непарне, одержимо

.

Приклад 2. Знайти

Розв`язання. Маємо інтеграл такого ж вигляду, як у попередньому прикладі, де n= 3>0 i непарне, тому

.

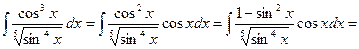
Приклад 3. Знайти

Розв`язання. Тут маємо інтеграл ІІІ типу (випадок в), де m= 2,

n=- 4<0 i парне, тому

.

Зауважимо, що даний інтеграл можна знайти простіше. Зробивши деякі тотожні перетворення підінтегрального виразу, одержимо

.

Приклад 4. Знайти

Розв`язання. Враховуючи, що m= 2, n= 4, тобто обидва показники додатні і парні, будемо мати

.

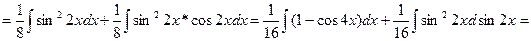
Приклад 5. Знайти

Розв`язання. І спосіб. Враховуючи, що будемо мати

.

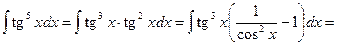
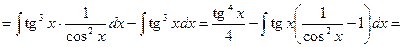
ІІ спосіб. Маємо

	–	t ^5		t ^2+1
t ^5+ t ^3		t ^3–t
=	–	– t ^3			=
– t ^3– t
		t

.

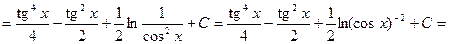
Приклад 6. Знайти

Розв`язання.

Якщо у виразі замінити cos x на - cos x, то дріб змінить знак на протилежний, тому тут треба застосувати підстановку sin x=t. Тоді x= arcsin t, i

.

Приклад 7. Знайти

Розв`язання. Оскільки при зміні знаків у sin x i cos x підінтегральна функція не змінює знака, то застосовуємо підстановку tg x=t.

Отже, маємо

.

Приклад 8. Знайти

Розв`язання. Підінтегральна функція є раціональною фуекцією від sin x i cos x. Тому, зробивши підстановку одержимо

.

Приклад 9. Знайти

Розв`язання. Діючи, як у попередньому прикладі, будемо мати

.

Приклад 10. Знайти

Розв`язання. Враховуючи, що 4-3cos² x +5sin² x= 4(cos² x+ sin² x)-

-3cos2 x+ 5sin² x=c os² x+ 9sin² x, одержимо

.

Приклад 11. Знайти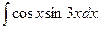

Розв`язання. Маємо інтеграл V типу. Застоcувавши формулу (28), згідно з якою 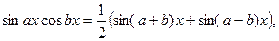одержимо

.

Приклад 12. Знайти

Розв`язання. Маємо

.

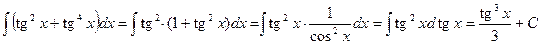Приклад 13. Знайти

Розв`язання.

.

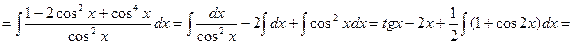
Приклад 14. Знайти

Розв`язання.

ВПРАВИ

Знайти інтеграли:

1. Відповідь: .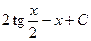

2. Відповідь: .

3. Відповідь: .

4. Відповідь: .

5. 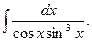Відповідь: .

6. 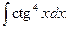Відповідь: .

7. Відповідь: .

8. Відповідь: .

9. Відповідь: .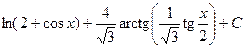

10. 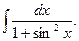Відповідь: .

11. Відповідь: .

12. Відповідь: .

13. Відповідь: .

14. Відповідь: .

15. Відповідь: .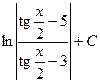

16. Відповідь: .

17.

Відповідь: .

Тригонометричні підстановки

Інтеграли вигляду

зводяться до інтегралів від раціональної відносно sin t i cos t функції за допомогою відповідної тригонометричної підстановки.

І. Для знаходження інтеграла застосовують підстановку x=a sin t (або x=a cos t).

ІІ. Для знаходження інтеграла треба покласти

x=a tg t (або x=a ctg t).

ІІІ. Для знаходження інтеграла замінюють (або ).

Дата добавления: 2015-10-30