
Читайте также:
|
Задача 1. Обчислити площу фігури, обмеженої лінією у=х (х– 1)2 і віссю О x.
Розв`язання. Функція у=х (х– 1)2 визначена для всіх дійсних значень х. Точки перетину графіка функції з віссю Оx знаходимо із системи рівнянь

звідки х 1 = 0, у 1 = 0і х 2=1, у 2=0.
 Таким чином, графік функції у=х (х– 1)2 перетинає вісь О x в точках (0;0) і (1;0). Не важко переконатися в тому, що функція у=х (х– 1)2 має екстремум в точках
Таким чином, графік функції у=х (х– 1)2 перетинає вісь О x в точках (0;0) і (1;0). Не важко переконатися в тому, що функція у=х (х– 1)2 має екстремум в точках  і (1;0), а також точку перегину
і (1;0), а також точку перегину  . Читачеві пропонуємо перевірити це самостійно.
. Читачеві пропонуємо перевірити це самостійно.
На основі цих даних будуємо графік функції (рис.5).
Із рис.5 видно, що фігура обмежена зверху лінією у=х (х– 1)2, знизу у= 0 і проекціюється на вісь Ох у відрізок  . Отже ув=х (х– 1)2, ун= 0, а= 0, b= 1.
. Отже ув=х (х– 1)2, ун= 0, а= 0, b= 1.
Таким чином, за формулою (41б) маємо

Відзначимо, що площу одержаної фігури можна було б обчислити і за формулою (41а), бо ця фігура є криволінійна трапеція.
Задача 2. Обчислити площу фігури, обмеженої лінією  і параболою
і параболою 
 Розв`язання. Крива
Розв`язання. Крива  – парабола з вершиною в точці О (0;0) і віссю симетрії Оу. Вітки параболи напрямлені уверх (рис.6).
– парабола з вершиною в точці О (0;0) і віссю симетрії Оу. Вітки параболи напрямлені уверх (рис.6).
Крива  – локон Аньєзі. Із рівняння видно, що при будь- якому х функція набуває лише додатніх значень, а тому її графік розташований вище осі Ох, а вісь Оу є її віссю симетрії, бо у (–х) =у (х). Найбільше значення, яке дорівнює одиниці, функція набуває при х= 0, а при
– локон Аньєзі. Із рівняння видно, що при будь- якому х функція набуває лише додатніх значень, а тому її графік розташований вище осі Ох, а вісь Оу є її віссю симетрії, бо у (–х) =у (х). Найбільше значення, яке дорівнює одиниці, функція набуває при х= 0, а при 

Схематично графік цієї функції зображений на рис.6. Точніше побудувати графік цієї функції можна за допомогою загальної схеми дослідження функції. Фігура, обмежена даними лініями, також показана на рис.6.
Площу фігури обчислимо за формулою (41б):
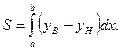
Для визначення меж інтегрування, знайдемо абсциси точок перетину ліній, розв`язуючи систему рівнянь:

Звідси х 1= –1, х 2=1. Отже, а= –1, b= 1.
Враховуючи також, що  , а
, а  будемо мати
будемо мати

а з урахуванням симетрії фігури відносно осі Оy

Задача 3. Знайти площу петлі лінії 
Розв`язання. Побудуємо графік лінії (рис.7). Фігура розташована симетрично відносно осі Оx, а тому досить знайти площу верхньої частини, яка розташована над віссю Оx, і результат подвоїти. Відрізок інтегрування  . Для обчислення площі фігури застосуємо формулу (41б). Підставляючи в цю формулу
. Для обчислення площі фігури застосуємо формулу (41б). Підставляючи в цю формулу  , ун= 0, а= 0, b= 1,одержимо
, ун= 0, а= 0, b= 1,одержимо

Задача 4. Обчислити площу фігури, обмеженої лініями у 2=2 х+ 1 і
х–у –1=0.
 |
Розв`язуючи систему рівнянь

знайдемо точки перетину прямої і параболи: А (0; –1), В (4;3).
Для обчислення площі заштрихованої фігури скористаємось формулою (41в), бо в разі використання формули (41б) фігуру треба було б розбити на дві частини, оскільки ун складається із двох різних ліній  і у=х – 1. Отже, підставляючи в формулу (41в) хп=у+ 1,
і у=х – 1. Отже, підставляючи в формулу (41в) хп=у+ 1,  і враховуючи, що
і враховуючи, що  , одержимо
, одержимо
 .
.
Вправи 
1. Обчислити площу фігури, обмеженої параболами у=х 2 і 
Відповідь: 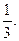
2. Обчислити площу криволінійної трапеції, обмеженої віссю абсцис і лінією 
Вказівка. Побудуйте лінію  надаючи аргументу х значень від 0 до 1.
надаючи аргументу х значень від 0 до 1.
Відповідь: 
3. Обчислити площу фігури, обмеженої лініями у=е–х, у=ех і прямою х= 1.
Відповідь: 
Об`єм тіла
 Якщо Q (x) – площа перерізу тіла площиною, перпендикулярною осі Оx в точці з абсцисою х (рис.9), то об`єм тіла обчислюється за формулою
Якщо Q (x) – площа перерізу тіла площиною, перпендикулярною осі Оx в точці з абсцисою х (рис.9), то об`єм тіла обчислюється за формулою
 (42a)
(42a)
де а і b – абсциси крайніх перерізів тіла.
Для обчислення об`ємів тіл обертання відносно координатних осей слід застосувати одну із наступних формул:

 (42б)
(42б)

 (42в)
(42в)

 (42г)
(42г)

 (42д)
(42д)

 (42е)
(42е)
Розв`язання задач
Задача 1. Обчислити об’єм трьохосьового еліпсоїда (рис. 15)


Розв’язання. В перерізі еліпсоїда площиною, паралельною площині xOz і віддаленої від неї на відстані у, одержимо еліпс

З півoсями
 i
i 
Відомо, що площа еліпса дорівнюї  . Отже, площа перерізу
. Отже, площа перерізу

Абсциси крайніх перерізів тіла відповідно дорівнюють – b і b. Тоді за формулою (42а) будемо мати
 .
.
Таким чином, об’єм еліпсоїда з півосями а, b і с дорівнює 
Зокрема, якщо а=b=с, еліпсоїд перетворюється в кулю, і в цьому випадку ми одержимо відому із елементарної математики формулу для обчислення об`єму кулі:

 де а – радіус кулі.
де а – радіус кулі.
Задача 2. Обчислити об’єм тіла, обмеженого поверхнею, яка утворюється обертанням параболи у 2=4 х навколо своєї осі (параболоїд обертання) і площиною, перпендикулярною до його осі і віддаленою від вершини параболи на відстані, рівній одиниці.
Розв’язання. Побудуємо тіло (рис.16).
Враховуючи, що 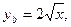 ун= 0, а= 0 і b= 1, за формулою (42г) будемо мати
ун= 0, а= 0 і b= 1, за формулою (42г) будемо мати
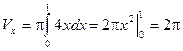
Отже, шуканий об’єм дорівнює  .
.
 Задача 3. Криволінійна трапеція, обмежена лінією у=хех і прямими х= 1 і у= 0, обертається навколо осі абсцис. Знайти об’єм тіла обертання.
Задача 3. Криволінійна трапеція, обмежена лінією у=хех і прямими х= 1 і у= 0, обертається навколо осі абсцис. Знайти об’єм тіла обертання.
Розв’язання. Побудуємо тіло обертання (рис.17). Об’єм одержаного тіла будемо обчислювати за формулою (42г), враховуючи, що ув=хех, ун= 0, а= 0 і b= 1:
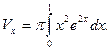
Використовуючи далі двічі формулу інтегрування частинами, будемо мати:



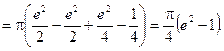
Таким чином, шуканий об’єм дорівнює 
 Задача 4. Обчислити об’єм тіла, одержаного обертанням фігури, обмеженої параболою у= 2 х-х 2 і віссю абсцис, навколо осі ординат.
Задача 4. Обчислити об’єм тіла, одержаного обертанням фігури, обмеженої параболою у= 2 х-х 2 і віссю абсцис, навколо осі ординат.
Розв’язання. Побудуємо тіло обертання (рис.18). Для обчислення об’єму тіла обертання скористаємось формулою (42е):

Враховуючи, що ув= 2 х–х 2, ун= 0 і  одержимо
одержимо
 .
.
Вправи
1. Фігура, обмежена дугами парабол у 2 =х і х 2 =у, обертається навколо осі абсцис. Знайти об’єм тіла обертання.
Відповідь: 
2 Обчислити об’єм тіла, яке одержуємо від обертання навколо осі ординат криволінійної трапеції, обмеженої дугою синусоїди y= sin x, яка відповідає півперіоду, і віссю абсцис.
Відповідь: 2 p 2.
3. Обчислити об’єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої лінією х 4 +у 4 =а 2 х 2.
Вказівка. Із рівняння лінії  . Враховуючи симетрію тіла відносно осі Оy, обчисліть половину об’єму для
. Враховуючи симетрію тіла відносно осі Оy, обчисліть половину об’єму для  , де
, де  , і результат подвойте.
, і результат подвойте.
Відповідь: 
4. Фігура, обмежена лініями y 2=(x+ 4)3 і х= 0, обертається навколо осі Оx. Знайти об’єм тіла обертання.
Відповідь: 
5. Знайти об’єм тіла, утвореного обертанням навколо осі ординат фігури, обмеженої лініями у 2 +х– 4=0 і х= 0.
Відповідь: 
6. Обчислити об’єм тіла, обмеженого еліптичним параболоїдом  і площиною у= 1.
і площиною у= 1.
Вказівка. Див. додаток.
Відповідь: 
7. Знайти об’єм тіла, обмеженого однопoлим гіперболоїдом 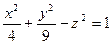 і площинами z= – 1 і z= 2.
і площинами z= – 1 і z= 2.
Вказівка. Див. додаток.
Відповідь: 
8.Обчислити об’єм тіла, обмеженого параболоїдом  і конусом
і конусом 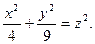
Вказівка. Див. додаток.
Відповідь: 
Економічний зміст визначеного інтеграла
Нехай функція  описує зміну в часі продуктивності деякого виробництва. Знайдемо об’єм продукції, виробленої за проміжок часу
описує зміну в часі продуктивності деякого виробництва. Знайдемо об’єм продукції, виробленої за проміжок часу  .
.
Якщо продуктивність не змінюється з часом ( - стала функція), то об’єм продукції
- стала функція), то об’єм продукції  ,віроблений за проміжок часу
,віроблений за проміжок часу  , задається формулою
, задається формулою  . У загальному випадку справедлива наближена рівність
. У загальному випадку справедлива наближена рівність  , де
, де  , яке виявляється тим точнішим, чим менше
, яке виявляється тим точнішим, чим менше  .
.
Розіб’ємо відрізок  на проміжки часу точками:
на проміжки часу точками:  . Для величини об’єму продукції
. Для величини об’єму продукції  , виготовленої за проміжок часу
, виготовленої за проміжок часу  , маємо
, маємо  , де
, де  ,
,  ,
, 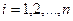 . Тоді
. Тоді
 .
.
Коли  прямує к нулю, тоді кожне із використаних наближених рівностей стає більш точнішим, тому
прямує к нулю, тоді кожне із використаних наближених рівностей стає більш точнішим, тому  .
.
Враховуючи означення визначеного інтегралу, остаточно одержуємо

тобто коли f(t) – продуктивність праці у момент t, то  є об’єм виробленої продукції за проміжок [0,T].
є об’єм виробленої продукції за проміжок [0,T].
Висновок: величина і об’єм продукції, виробленої за проміжок часу [0,T], чисельно дорівнює площі під графіком функції z = f(t), описуюча зміни продуктивність праці з спливанням часу, на проміжку [0,T] або  .
.
Застосування визначеного інтеграла для економічних розрахунків
Визначений інтеграл застосовують також для обчислення сумарних економічних ефектів. Розглянемо це на конкретному прикладі.
 Приклад 1. Нехай граничний прибуток МR за реалізацію продукції сталий і для конкретності МR = f (х) = 10 грн.,
Приклад 1. Нехай граничний прибуток МR за реалізацію продукції сталий і для конкретності МR = f (х) = 10 грн.,
де х — кількість проданих одиниць продукції. Визначити прибуток від продажу 1500 проданих одиниць продукції.
Розв’язання. Маємо 
З іншого боку, виходячи з означення граничного прибутку і первісної функції,
 =15000грн.
=15000грн.
Зауважимо, що обчислення загального доходу через визначений інтеграл є більш загальним, оскільки граничний ефект, як правило, залежить від х.
Графічно розглянутий приклад ілюструє рис. 19.
 Приклад 2. Фонди однієї організації зростають завдяки щорічним кампаніям літніх таборів для малозабезпечених. Витрати на кампанію становлять 10 000 грн. щодня. Відомо, що внески великі на початку кампанії, надалі вони спадають. Функція, яка описує отримання внесків за один день, має вигляд
Приклад 2. Фонди однієї організації зростають завдяки щорічним кампаніям літніх таборів для малозабезпечених. Витрати на кампанію становлять 10 000 грн. щодня. Відомо, що внески великі на початку кампанії, надалі вони спадають. Функція, яка описує отримання внесків за один день, має вигляд
с (t)= - 100 t 2 + 20 000, де t — кількість днів, а с (t) — внески за день. Організація хоче максимально збільшити отриману суму доходу.
Визначити, скільки часу треба проводити кампанію для отримання максимальної суми доходу.
Чому дорівнюють загальні витрати на кампанію?
Чому дорівнюють загальні внески?
Чому дорівнює дохід, що очікується?
Розв’язання. Розв'яжемо задачу за допомогою графіків.
Щоденні витрати на кампанію
l (t) =10000 грн.
На рис. 20 зображено дві функції: витрат на кампанію l (t)і внесків с (t). Поки рівень внесків перевищує рівень витрат, дохід є позитивним. Він буде позитивним до того часу, поки графіки функцій не перетнуться. Далі витрати перевищують внески. Дві функції перетинаються, коли
с (t) = l (t): 20000-100 ∙t 2 = 10000; 10000=100 ∙t2; t2= 100; t= 10 днів.
Загальні витрати на компанію за t= 10 днів
Е = 10000·10 = 100 000 грн.
Внески за 10 днів - площа під кривою між t =0 і t= 10:
С =  = 166666,67 грн.
= 166666,67 грн.
Сума очікуваного доходу: 
166666,67 - 100000 = 66666,67 грн.
Приклад 3. Лікарня оцінює, що людська кров надходить у її банк на рівні d (t) літрів щомісяця, причому d (t) =500(е- 0,4 t + 0,1), де t - тривалість надходження крові у місцях. Коли лікарня одержить 1000 л. крові?
Розв’язання. Площа під графіком d на рис. 21 характеризує загальне надходження крові. Лікарня одержить 1000 л. крові, коли
 .
.
Отже,
50 T+ 1250 ( 1– e -0,4 T )=1000  25 e- 0,4T = 5 + T.
25 e- 0,4T = 5 + T.
Розв'язавши це рівняння графічно, знайдемо Т ≈ 2,88 міс.
 Приклад 4. Компанія пропонує збудувати ядерну електростанцію на околиці столиці. Як і очікувалося, громадська думка з цього приводу розділилася. Одна група, яка виступає проти будівництва станції, зібрала дані, що стосуються обставин катастрофи на ній. Вона оцінює рівень смертей, які можуть трапитися від радіоактивних викидів, функцією r (t) = 200 е- 0,4 t ,
Приклад 4. Компанія пропонує збудувати ядерну електростанцію на околиці столиці. Як і очікувалося, громадська думка з цього приводу розділилася. Одна група, яка виступає проти будівництва станції, зібрала дані, що стосуються обставин катастрофи на ній. Вона оцінює рівень смертей, які можуть трапитися від радіоактивних викидів, функцією r (t) = 200 е- 0,4 t ,
де r (t) — рівень смертей (тис. людей за 1 годину), а t - час від початку аварії (в годинах). Населення столиці становить 1,5 млн. осіб.
Визначити очікувану кількість смертей за 1 годину після аварії на станції. За скільки часу після аварії за прогнозами місто вимре?
Розв’язання. Побудуємо графік функції r (t) (рис. 22).
Графік показує, що площа під ним між будь-якими двома точками t 1 і t 2 є мірою очікуваного рівня смертей протягом певного часу. Таким чином, протягом першої години очікується загиблих
 тис. осіб.
тис. осіб.
Усе населення міста загине після Т год., тобто


 , звідки Т = 14 год.
, звідки Т = 14 год.
Отже, за прогнозами місто вимре за 14 год.
Приклад 5. Одним із критеріїв вартості є ціна p, яку готовий заплатити споживач. Згідно з економічними законами купують товар за правилами ринку.
На рис. 23 зображено графіки функцій попиту q = р 2-40 р+ 400і пропозиції s= 10∙ р. Зрівноважена ціна 10 грн. настає тоді, коли попит становить 100 одиниць товару. Дохід за продану продукцію для виробника дорівнює в цьому випадку 10∙100=1000 грн. і визначається площею прямокутника ОВСЕ.
Однак, якщо розглянути природу функції попиту, то має економічний зміст ціна одиниці товару, більша за 10 грн., і знайдуться покупці, які куплять товар за ціною між 10 і 20 грн., особливо тоді, коли попит перевищує пропозицію.
Економісти стверджують, що мірою справжньої корисності продукту є площа фігури ОВСО.
Вартість, що відповідає заштрихованій площі СDЕ, називається додатковою вартістю, ї можна визначити за допомогою інтеграла
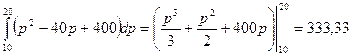 грн.
грн.
Отже, додаткова вартість для споживача дорівнює 333,33 грн.
Якщо в функції Коба-Дугласа вважати, що витрати праці є лінійно залежні від часу, а витрати капіталу незміні, то вона прийме вигляд g (t) = (αt+β)eγt. Тоді об’єм виробленої продукції за T років буде складати:
 . (43)
. (43)
Приклад 6. Знайти об’єм продукції, виробленої за 4 роки, якщо в функції Коба-Дугласа має вигляд g (t)=(t +1) e 3 t .
Розв’язання. За формулою (43) об’єм Q виробленої продукції дорівняє
 .
.
Скористаємось методом інтегрування частинами.
Покладемо u = t+ 1, dv=e 3 t dt, du=dt, v=  . Отже,
. Отже,
 (умов. од.)
(умов. од.)
 Досліджуємо криву Лоренцо – залежність відсотка прибутку від відсотка населення, яке має цей прибуток (крива ОВА, рис. 24), ми можемо оцінити степінь нерівності у розподілі прибутку населення. При рівномірному розподілу прибутку крива Лоренцо вироджується в пряму – бісектрису ОА, тому площа фігури ОАВ між бісектрисою ОА і кривою Лоренцо, віднесена до площі трикутника ОАС (коефіцієнт Джини), характеризує степінь нерівності у розподілі прибутку населення.
Досліджуємо криву Лоренцо – залежність відсотка прибутку від відсотка населення, яке має цей прибуток (крива ОВА, рис. 24), ми можемо оцінити степінь нерівності у розподілі прибутку населення. При рівномірному розподілу прибутку крива Лоренцо вироджується в пряму – бісектрису ОА, тому площа фігури ОАВ між бісектрисою ОА і кривою Лоренцо, віднесена до площі трикутника ОАС (коефіцієнт Джини), характеризує степінь нерівності у розподілі прибутку населення.
Приклад 7. За даними дослідження розподілу прибутків в одній із країн крива Лоренцо ОВА (рис. 24.) може бути описано рівнянням  , де х – доля населення, у – доля прибутку населення. Обчислити коефіцієнт Джини.
, де х – доля населення, у – доля прибутку населення. Обчислити коефіцієнт Джини.
Розв’язання. Очевидно, коефіцієнт Джини (див. рис.24.)

Тому  За допомогою заміни x= sin t, можна обчислити
За допомогою заміни x= sin t, можна обчислити  . Отримуємо, коефіцієнт Джини
. Отримуємо, коефіцієнт Джини  .
.
Достане високе значення к свідчить про суттєву нерівномірність розподілу прибутків населення в даній країні.
Визначення початкової суми за її кінцевою величиною, отриманої за час t (років) при річному відсотку (відсоткової ставки) р, називається дисконтуванням. Задачі такого виду зустрічаються при означенні економічної ефективності капітулу вкладення.
Нехай Кt – кінцева сума, отримана за t років, і К – дисконтована (початкова) сума, яку у фінансовому аналізі має назву сучасна сума. Коли відсотки прості, тоді Кt = К (1 + і t),де і=р/ 100 – питомавідсоткова ставка. Одержуємо, К= Кt /(1 + і t). У випадку складних відсотків маємо: Кt=К (1 + і t) t і тому К=Кt/ (1 + і t) t.
Нехай щорічне надходження прибутку змінюється з часом і описується функцією f (t) і при питомій нормі відсотку, яка дорівнює і, відсоток нараховується безперервно. Можна показати, що в цьому випадку дисконтований дохід К за час Т обчисляється за формулою:
 . (44)
. (44)
Приклад 8. Знайти дисконтований прибуток за 3 роки при відсотковій ставці 8 %, якщо первісне (базове) капіталовкладення складає 10 млн. грн., і намічається щорічне збільшення капіталовкладення на 1 млн. грн.
Розв’язання. Очевидно, що капіталовкладення задаються функцією f(t)= 10 + 1 ∙t= 10 +t. Тоді за формулою (44) дисконтована сума капіталовкладення:

Скориставшись методом інтегрування частинами, отримуємо К= 30,5 млрд. грн. Це означає, що для отримання однаково нарощеної суми за 3 роки щорічних капіталовкладень від 10 до 13 млн. грн.. при тій же відсотковій ставці, яка неперервна нараховується.
Нехай відома функція t=t (x), яка описує витрати часу t на вироблення виробу в залежності від степені освоювання виробництва, де х – порядковий номер у партії. Тоді середній час tср, який був витрачений на виготовлення одного виробу у період засвоювання від х 1 до х 2виробів, обчислюється за теоремою про середнє (31):
 (45)
(45)
Що до функції зміни витрат часу на виготовлення виробів t=t (x),то вона часто має вигляд:
tcp= ax-b, ( 46)
де а – витрати на перший виріб, b – показник виробничного процесу.
Приклад 9. Знайти середній час tср, який був витрачений на виготовлення одного виробу у період засвоювання від х 1 = 100 до х 2 = 121 виробів, покладаємо у формулі (46) а= 600 (хв.), b= 0,5.
Розв’язання. Скористаємось формулою (45), отримуємо
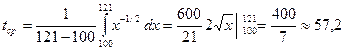 (хв.).
(хв.).
ДОДАТКИ
Додаток 1
Знайти інтеграли:
Варіант 1
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5. 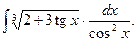 10.
10. 
Варіант 2
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 3
1.  6.
6. 
2.  7.
7. 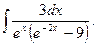
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 4
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 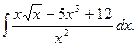
4.  9.
9. 
5.  10.
10. 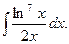
Варіант 5
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  . 10.
. 10. 
Варіант 6
1.  6.
6. 
2.  7.
7. 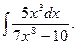
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 7
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 8
1.  6.
6. 
2.  7.
7. 
3. 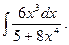 8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 9
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 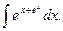
5.  10.
10. 
Варіант 10
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 11
1.  6.
6. 
2. 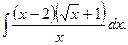 7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 12
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 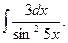
4.  9.
9. 
5. 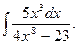 10.
10. 
Варіант 13
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4. 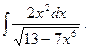 9.
9. 
5.  10.
10. 
Варіант 14
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 15
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4. 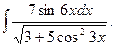 9.
9. 
5.  10.
10. 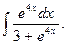
Варіант 16
1.  6.
6. 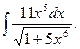
2.  7.
7. 
3.  8.
8. 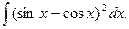
4.  9.
9. 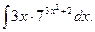
5.  10.
10. 
Варіант 17
1. 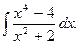 6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5. 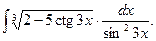 10.
10. 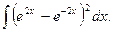
Варіант 18
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 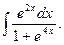
Варіант 19
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 20
1.  6.
6. 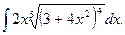
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5. 
 10.
10. 
Варіант 21
1. 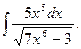 6.
6. 
2.  7.
7. 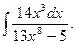
3.  8.
8. 
4.  9.
9. 
5. 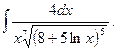 10.
10. 
Варіант 22
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4. 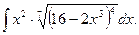 9.
9. 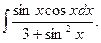
5. 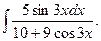 10.
10. 
Варіант 23
1.  6.
6. 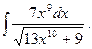
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 24
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 25
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 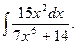
4.  9.
9. 
5. 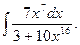 10.
10. 
Варіант 26
1.  6.
6. 
2.  7.
7. 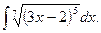
3.  8.
8. 
4.  9.
9. 
5. 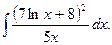 10.
10. 
Варіант 27
1.  6.
6. 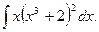
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 28
1. 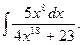 6.
6. 
2.  7.
7. 
3.  8.
8. 
4. 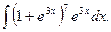 9.
9. 
5.  10.
10. 
Варіант 29
1.  6.
6. 
2.  7.
7. 
3. 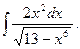 8.
8. 
4.  9.
9. 
5.  10.
10. 
Варіант 30
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9.
Дата добавления: 2015-10-30; просмотров: 282 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Розв`язання прикладів | | | Тематика курсовых проектов и работ. |