Розв`язання прикладів. Приклад 1. Знайти

Приклад 1. Знайти

Розв`язання. Маємо інтеграл від елементарного дробу І типу. Покладемо 3x+2=t, тоді 3dx=dt i тому

.

Розв`язання цього ж прикладу можна записати ще й так:

.

Приклад 2. Знайти

Розв`язання. Маємо інтеграл від елементарного дробу ІІ типу. Оскільки

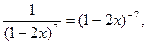i то

.

Приклад 3. Знайти

Розв`язання. Маємо інтеграл від елементарного дробу ІІІ типу, де А=0, В=1, Виділивши повний квадрат із квадратного тричлена 4х²+4х+5, одержимо табличний інтеграл (17). Дійсно

.

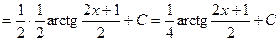Приклад 4. Знайти

Розв`язання. Як і в попередньому прикладі маємо також інтеграл від елементарного дробу третього типу, де А =-8, В =7, D=b²-4ac =-20<0. Спочатку виділимо похідну знаменника в чисельнику дробу. Для цього чисельник подамо у вигляді

.

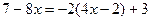Тоді

.

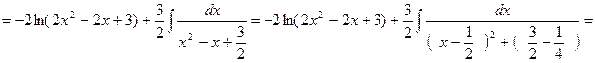
Тут взято за формулою (6) таблиці інтегралів, вважаючи

u=2x²-2x+3 i враховуючи, що 2 х ² - 2 х+ 3 > 0 для будь-якого х, а -

за формулою (17), вважаючи i враховуючи, що

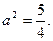
Покажемо тепер інший спосіб розвязання цього ж прикладу.

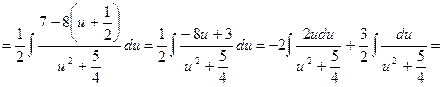
де 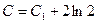, бо .

Відзначимо, що інтеграл виду

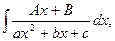
де квадратний тричлен ах²+вх+с має дискримінант D=b²-4ac 0 можна знаходити аналогічно знаходженню інтеграла від елементарного дробу ІІІ типу.

Приклад 5. Знайти

Розв`язання. Підінтегральна функція являє собою правильний раціональний дріб, знаменник якого х<sup>2</sup>+6х+9=(х+3)<sup>2</sup>, бо D=b<sup>2</sup>-4ac=0. Тому цей дріб можна подати у вигляді суми двох елементарних дробів ІІ типу. Однак простіше розв`язати цей приклад таким же способом, яким розв`язано попередній приклад.

Отже, маємо

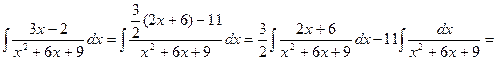
Приклад 6. Знайти

Розв`язання. І спосіб. Маємо

ІІ спосіб. Підінтегральний дріб являє собою правильний раціональний дріб, але не найпростіший, бо квадратний тричлен х²+х- 6 має два дійсні корені і , так як його дискримінант D=b²-4ac= 1+24=25>0. Тому цей квадратний тричлен можна розкласти на множники , а підінтегральний правильний раціональний дріб на суму двох елементарних дробів І типу, тобто подати у вигляді

або

Звільняючись від дробових членів, для чого помножимо обидві частини рівності на добуток , одержимо

,

або

.

Прирівнюючи коефіцієнти при однакових степенях х в лівій і правій частинах тотожності, одержимо систему двох лінійних рівнянь з двома невідомими

Розв`язавши цю систему, знаходимо невизначені коефіцієнти i

Таким чином,

a

Приклад 7. Знайти

Розв`язання. Підінтегральний дріб неправильний, бо степінь многочлена чисельника більший, ніж степінь многочлена знаменника. Тому виділимо спочатку цілу частину, поділивши многочлен чисельника на многочлен знаменника

–	x ^5+ x ^4-8		x ^3-4 x
x ^5–4 x ^3		x ^2+ x +4	(ціла частина)
–	x ^4+4 x ^3-8
x ^4–4 x ^2
–	4 x ^3+4 x ^2-8
4 x ^3–16 x
	4 x ^2+16 x -8	(остача).

Тепер подамо підінтегральний дріб у вигляді суми цілої частини і правильного дробу, тобто

Тоді

В інтегралі, який залишився, підінтегральний дріб (правильний і нескоротний) розкладемо на елементарні дроби. Оскільки знаменник дробу х ³-4 х=х (х ²-4) =

=х (х -2)(х +2) має три прості корені х= 0, х= 2 і х = -2, то його можна подати у вигляді суми трьох дробів І типу, тобто

Звільнюючись від дробових членів, одержимо

х ²+4 х -2= А (х -2)(х +2)+ Вх (х +2)+ Сх (х -2)

або

х ²+4 х -2=(А+В+С) х ²+(2 В- 2 С) х- 4 А.

Прирівнюючи коефіцієнти при однакових степенях х в обох частинах одержаної тотожності, одержимо систему рівнянь для визначення коефіцієнтів А, В, С:

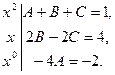
Розв`язавши цю систему, знаходимо

Слід відзначити, що тут коефіцієнти А, В і С простіше було б знайти способом підстановки в тотожність частинних значень х, в якості яких доцільно взяти корені знаменника, тобто:

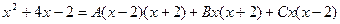
звідки

Таким чином,

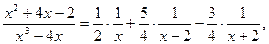
а шуканий інтеграл

Приклад 8. Знайти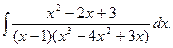

Розв`язання. Переконуємося, що підінтегральний дріб- правильний і нескоротний. Враховуючи, що

(х -1)(х ³-4 х ²+3 х)= х (х -1)(х ²-4 х +3) =х (х -1)(х -1)(х -3) =х (х -1)²(х -3)

має чотири корені, із яких два х= 0 і х= 3- прості, а х= 1- двократний, подамо дріб у вигляді суми чотирьох елементарних дробів:

Звільняючись від дробових членів, одержимо тотожність для знаходження коефіцієнтів A, B, C, D:

x ²-2 x +3= A (x -3)(x -1)²+ Bx (x -1)² +Cx (x -3) +Dx (x -1)(x -3).

Коефіцієнти знаходимо комбінованим способом

Звідси

Отже,

а шуканий інтеграл

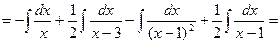
ВПРАВИ

Знайти інтеграли:

1.

Відповідь: .

2.

Відповідь: .

3.

Відповідь: .

4.

Відповідь: .

5.

Відповідь: .

6.

Відповідь: .

7.

Відповідь: .

8.

Відповідь: .

9.

Відповідь: .

Дата добавления: 2015-10-30