
|
Читайте также: |
Приклад 1. Оцінити інтеграл  .
.
Розв`язання.  – неперервна функція на відрізку
– неперервна функція на відрізку  . Знайдемо її найменше і найбільше значення на цьому відрізку. Для цього знайдемо
. Знайдемо її найменше і найбільше значення на цьому відрізку. Для цього знайдемо  :
:

Прирівнюючи  до нуля, одержимо х 1=1 Î
до нуля, одержимо х 1=1 Î  і х 2=9 Ï
і х 2=9 Ï  Похідна не існує в точках
Похідна не існує в точках  Ï
Ï  .
.
Обчислимо значення функції  при х= 0, х =1 і х= 2:
при х= 0, х =1 і х= 2:

Отже, найбільше значення функції  на відрізку
на відрізку  дорівнює 0,6, а найменше – 0,5.
дорівнює 0,6, а найменше – 0,5.
Таким чином,

або

Зауважимо, що точне значення даного інтеграла можна знайти за формулою Ньютона – Лейбніца, згідно з якою
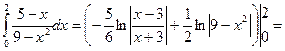

Приклад 2. Обчислити середнє значення функції f (x) = 2 x 2+3 x+ 3 на відрізку  .
.
Розв`язання. За теоремою про середнє значення визначеного інтеграла
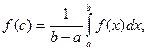
де f (c) - середнє значення функції f (x) на відрізку  . Оскільки b-а =4-1 =3і
. Оскільки b-а =4-1 =3і
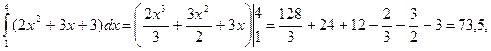
то


Таким чином, середнє значення функції f (x) = 2 x 2+3 x+ 3 на відрізку  дорівнює 24,5.
дорівнює 24,5.
Приклад 3. Обчислити 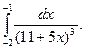
Розв`язання. За формулою Ньютона – Лейбніца
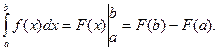
Отже, скориставшись цією формулою і властивістю 5 визначеного інтеграла, одержимо
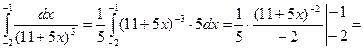

Приклад 4. Обчислити  .
.
Розв`язання. На підставі формули (30) і властивості 6 визначеного інтеграла, будемо мати
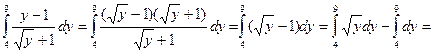

Приклад 5. Обчислити 
Розв`язання. Згідно з формулою (30) і властивостями 5 і 6 визначеного інтеграла, будемо мати


 .
.
Приклад 6. Обчислити 
Розв`язання. В силу формули Ньютона – Лейбніца


Приклад 7. Обчислити  .
.
Розв`язання.

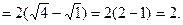
Приклад 8. Обчислити  .
.
Розв`язання.

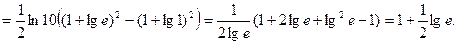
Приклад 9. Обчислити  .
.
Розв`язання.
 =
= 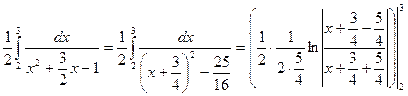
 .
.
Приклад 10. Обчислити  .
.
Розв`язання.
 =
= 
 .
.
ВПРАВИ
Обчислити інтеграли:
1.  Відповідь:
Відповідь:  .
.
2.  Відповідь:
Відповідь:  .
.
3.  Відповідь:
Відповідь:  .
.
4. 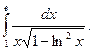 Відповідь:
Відповідь:  .
.
5.  Відповідь:
Відповідь:  .
.
6.  Відповідь:
Відповідь:  .
.
7.  Відповідь:
Відповідь:  .
.
8.  Відповідь:
Відповідь:  .
.
9.  Відповідь:
Відповідь:  .
.
10.  Відповідь:
Відповідь:  .
.
11.  Відповідь: 2.
Відповідь: 2.
12.  Відповідь:
Відповідь:  .
.
13.  . Відповідь:
. Відповідь: 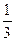 .
.
14.  Відповідь:
Відповідь:  .
.
15.  Відповідь:
Відповідь: 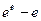 .
.
16.  Відповідь: ln(e +1).
Відповідь: ln(e +1).
17.  Відповідь: 1-cos1.
Відповідь: 1-cos1.
18.  Відповідь:
Відповідь:  .
.
19. Оцінити інтеграл  Відповідь:
Відповідь: 
20. Оцінити інтеграл  Відповідь: 0 < I < 1.
Відповідь: 0 < I < 1.
2.4. Заміна змінної у визначеному інтегралі
Якщо функція f(x) неперервна на відрізку  і
і  -функція неперервна зі своєю похідною першого порядку на відрізку
-функція неперервна зі своєю похідною першого порядку на відрізку  , причому
, причому  для
для  , то
, то
 (32)
(32)
Формулу (32) називають формулою заміни змінної для визначеного інтеграла.
Із сказаного випливає, що функція  на відрізку
на відрізку  повинна бути монотонною або іншими словами всі значення функції
повинна бути монотонною або іншими словами всі значення функції  повинні знаходитися на відрізку
повинні знаходитися на відрізку  .
.
Зауважимо, що заміна змінної у визначеному інтегралі вимагає обережності і обов'язкового виконання всіх перерахованих умов, накладених на функцію 
Відзначимо також, що зробивши заміну змінної у визначеному інтегралі для його обчислення, немає необхідності переходити до початкової змінної, як це ми робили при знаходженні невизначеного інтеграла, а досить лише перерахувати межі інтегрування для нової змінної.
Для цього у рівність  замість х підставляємо по черзі нижню межу
замість х підставляємо по черзі нижню межу  і верхню межу
і верхню межу  інтегрування і розв`язуємо рівняння
інтегрування і розв`язуємо рівняння  і
і  . Знайдені значення t і будуть відповідно нижньою
. Знайдені значення t і будуть відповідно нижньою  і верхньою
і верхньою  межами інтегрування для нової змінної інтегрування. Якщо кожне із рівнянь
межами інтегрування для нової змінної інтегрування. Якщо кожне із рівнянь  і
і  задовольняє не одно, а декілька значень t, то за
задовольняє не одно, а декілька значень t, то за  і
і  можна прийняти будь –яке із них. Однак вільність вибору обмежується вимогою, щоб значення функції
можна прийняти будь –яке із них. Однак вільність вибору обмежується вимогою, щоб значення функції  не виходили із відрізка
не виходили із відрізка  , на якому визначена і неперервна підінтегральна функція f (x).
, на якому визначена і неперервна підінтегральна функція f (x).
Ще раз застерігаємо, що невиконання всіх указаних вимог, накладених на функцію  , може привести до грубих помилок.
, може привести до грубих помилок.
У багатьох випадках доводиться замість підстановки  , покладати
, покладати  . У цьому випадку нові межі інтегрування
. У цьому випадку нові межі інтегрування 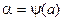 і
і  . Якщо із
. Якщо із  випливає, що
випливає, що  , то для функції
, то для функції  повинні виконуватися всі указані вище умови.
повинні виконуватися всі указані вище умови.
Дата добавления: 2015-10-30; просмотров: 404 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Розв`язання прикладів | | | Розв`язання прикладів |