Розв`язання прикладів. Приклад 1. Обчислити невласний інтеграл

Приклад 1. Обчислити невласний інтеграл

Розв`язання. Підінтегральна функція не визначена в точках x ₁= –1 і x ₂=1, причому при і функція необмежено зростає. Таким чином, маємо невласний інтеграл від необмеженої функції. За означенням

Зауважимо, що замість точки x= 0 можна було б взяти будь-яку іншу внутрішню точку відрізка

Приклад 2. Показати, що невласний інтеграл збігається.

Розв`язання. Підінтегральна функція не обмежена в будь-якому околі точки x= 0 неперервна при 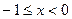і . Отже маємо невласний інтеграл від необмеженої функції.

Так як первісна функція неперервна в точці x= 0, то на основі формули (40) одержимо

Таким чином, даний інтеграл збігається.

Зауважимо, що скориставшись означенням (37), одержимо такий самий результат. Дійсно,

.

Не важко зрозуміти, що застосування формули (40) для розв`язання цього прикладу, привело до більш простіших викладок.

Приклад 3. Обчислити за означенням невласний інтеграл або установити його розбіжність.

Розв`язання. Підінтегральна функція не обмежена в околі точки х= 1. На будь-якому ж відрізку вона інтегровна, так як є неперервною функцією. Тому за означенням

Отже, даний інтеграл збігається.

Зауважимо, що розв`язати цей приклад можна і за формулою (40), бо функція неперервна на відрізку і диференційовна в кожній точці проміжка 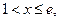причому на цьому проміжку. Тому

Приклад 4. Обчислити невласний інтеграл 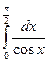або установити його розбіжність.

Розв`язання. Підінтегральна функція 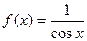необмежена в околі точки і інтегровна на будь- якому відрізку як неперервна функція. Тому

Отже, даний інтеграл розбігається.

Приклад 5. Обчислити невласний інтеграл або установити його розбіжність.

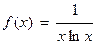Розв`язання. Підінтегральна функція не визначена в точці х= 1, яка співпадає з нижньою межею інтегрування, причому при функція необмежено зростає. Тому за означенням

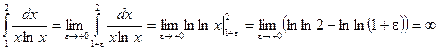
Таким чином, даний інтеграл розбігається.

Приклад 6. Обчислити невласний інтеграл або установити його розбіжність.

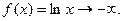Розв`язання. При підінтегральна функція Тому

Застосовуючи формулу інтегрування частинами, знаходимо

Таким чином, шуканий інтеграл

Оскільки одержали скінченну границю, то даний інтеграл збігається.

Приклад 7. Обчислити невласний інтеграл

Розв`язання. Виконуючи нескладні перетворення інтеграла, одержимо

У першому із одержаних інтегралів підінтегральна функція неперервна на відрізку тому за формулою Ньютона –Лейбніца

Другий інтеграл невласний, бо підінтегральна фунуція при За означенням

Отже, остаточно маємо

Зазначимо, що даний інтеграл можна розв`язати ще й так:

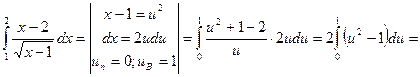
Як бачимо, після заміни змінної у невласному інтегралі, одержали визначений інтеграл.

Приклад 8. Дослідити на збіжність інтеграл

Розв`язання. Підінтегральна функція є нескінченно великою при Отже маємо невласний інтеграл. Подамо цю функцію у вигляді

При множник 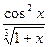прямує до сталої величини і тому порядок цієї нескінченно великої функції при порівняно з дорівнює Таким чином, на основі ознаки 2 даний інтеграл збігається.

Приклад 9. Дослідити на збіжність інтеграл

Розв`язання. Підінтегральна функція в проміжку інтегрування додатна і при . Враховуючи, що при ~ а ~ sin x ~ x, будемо мати

тобто f (x) є нескінченно великою порядку порівняно з . Отже, на основі ознаки 2 даний інтеграл збігається.

Приклад 10. Довести, що інтеграл збігається.

Розв`язання. Маємо невласний інтеграл, бо при підінтегральна функція Оскільки для і інтеграл збігається, то в силу ознаки 3 збігається і інтеграл а отже, збігається і до того ж абсолютно, заданий інтеграл.

Приклад 11. Установити збіжність інтеграла і обчислити його.

Ров`язання. При підінтегральна функція Застосувавши метод інтегрування частинами, одержимо

тому що

Оскільки то інтеграл є визначеним.

Отже, вихідний інтеграл збігається.

Для обчислення вихідного інтеграла зробимо підстановку x=2t. Тоді dx= 2 dt, t_H = 0, i

В останньому інтегралі зробимо підстановку Тоді dt= – dz, і

Таким чином,

Звідси

Приклад 12. Обчислити невласний інтеграл або установити його розбіжність.

Розв`язання. Підінтегральна функція не існує в точках і При функція . Отже,

Обчислюючи перший інтеграл, одержимо

Так як одержана границя нескінченна, то цей інтеграл розбігається. Другий інтеграл обчислювати не потрібно, бо на основі oзначення невласний інтеграл розбігається, якщо принаймні один із інтегралів розбігається. Таким чином, вихідний інтеграл розбігається.

Вправи

Обчислити невласні інтеграли або установити їх розбіжність:

1. Відповідь:

2. Відповідь:

3. 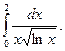Відповідь: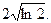

4. 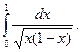Відповідь:

5. Відповідь: розбігається.

6. Відповідь:

7. 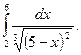Відповідь: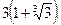

8. Відповідь: розбігається.

9. Відповідь: розбігається.

10. Відповідь:

11. Відповідь:

12. Відповідь:

Дослідити на збіжність невласні інтеграли:

13. Відповідь: збігається.

14. Відповідь: розбігається.

15. Відповідь: розбігається.

16. Відповідь: збігається.

17. Відповідь: розбігається.

18. Відповідь: розбігається.

19. Відповідь: збігається.

20. Відповідь: збігається.

Питання до самоперевірки

1. Що називають невласним інтегралом від даної функції з нескінченними проміжками інтегрування? Дати геометричне тлумачення і навести приклади збіжних і розбіжних інтегралів.

2. Сформулювати і довести ознаки збіжності невласних інтегралів з нескінченними проміжками інтегрування.

3. Який невласний інтеграл називають абсолютно збіжним і який умовно збіжним?

4. Що називають невласним інтегралом від розривної функції на данному скінченному проміжку інтегрування? Дати геометричне тлумачення і навести приклади збіжних і розбіжних інтегралів.

5. Сформулювати і довести ознаки збіжності невласних інтегралів від необмежених функцій.

6. Як виконується заміна змінної у невласному інтегралі?

7. У якому випадку невласний інтеграл від необмеженої функції можна обчислити безпосередньо за формулою Ньютона –Лейбніца?

Вправи

Дослідити на збіжність невласні інтеграли, обчислюючи їх безпосередньо

(за означенням) або скориставшись ознаками збіжності:

1. Відповідь: розбігається.

2. Відповідь: розбігається.

3. Відповідь: збігається.

4. Відповідь: збігається.

5. Відповідь: збігається.

6. Відповідь: розбігається.

7. 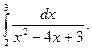Відповідь: розбігається.

8. Відповідь: розбігається.

9. Відповідь: збігається.

10. Відповідь: збігається.

11. Відповідь: розбігається.

12. Відповідь: розбігається.

13. Відповідь: розбігається.

14. Відповідь: розбігається.

15. Відповідь: розбігається.

16. Відповідь: збігається.

17. 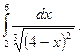Відповідь: збігається.

18. Відповідь: розбігається.

19. Відповідь: збігається.

20. Відповідь: розбігається.

Дата добавления: 2015-10-30