Автоматичний вибір кроку інтегрування

Розглянемо питання про автоматичний вибір кроку інтегрування. Можливість контролювати на кожному кроці точність обчислень дозволяє дуже економічно обчислювати інтеграл з заданою точністю eps. Розіб'ємо первинний відрізок інтегрування [а,b] на деяке число невелике частин [ x_{i -1}, x_i ], i=1, 2, …, m. Тепер застосуємо до кожного відрізка [ x_{i -1}, x_i ], квадратурну формулу Симпсона з кроком h і h/2. В результаті обчислимо значення інтегралів по відрізку [ x_{i -1}, x_i ]: I_h,i та I_h/2,i. Якщо виконуватиметься нерівність: ½I_h,i-I_h/2,i½/15£e/m або в загальному випадку ½I_h,i-I_h/2,i½/15£e½x_i-x_i-1½/(b-a), то задана точність чисельного інтегрування по відрізку [ x_{i -1}, x_i ] досягнута. Якщо ж нерівність не виконується, то необхідно обчислити той же інтеграл по тому ж відрізку з кроком h/2 і h/4 і знову повторити перевірку ітд. Таким чином, первинні відрізки швидкої зміни функції розбиваються на більше число відрізків інтегрування, а відрізки плавнішої зміни функції - на менше.

Приклад. Розглянемо функцію ln(x) на [а,b]:

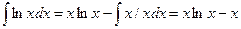. Якщо узяти b=1, a=10^-5 і підставити межі інтегрування, то I=0+1.1151293*10^-4-(b-a)»-0.9998748. При прямуванні х до нуля похідні підінтегральної функції швидко ростуть. А саме, друга похідна 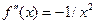, четверта 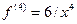. Тому, для того, щоб обчислити інтеграл з високою точністю, поблизу нуля необхідно збільшити число розбиття відрізку. Якщо спочатку розбити відрізок на 10 частин, і обчислювати інтеграл з точністю до 10^-12, то по методу Симпсона з автоматичним вибором кроку необхідно перший відрізок (від нуля) розбити на 262144 частин, другий на 256, 3 на 128, відрізки 4-7 на 64 частини і відрізки 8-10 на 32 частини. По попередньому алгоритму було б необхідно розбити весь відрізок інтегрування на 262144 частини. Таким чином, виграш складає приблизно 10 разів.

Блок-схема методу чисельної інтегрування з автоматичним вибором кроку відрізняється тільки головною програмою. Спочатку вводиться відрізок інтегрування, точність розрахунку інтеграла і інформація про первинне розбиття інтервалу на відрізки, до яких буде застосований алгоритм автоматичного вибору кроку. У нашому випадку весь відрізок розбивається на рівні відрізки, їх число задається значенням змінної m. Загальне значення інтеграла зберігатися в змінній Int. Тепер можна застосувати алгоритм апостеріорної оцінки погрішності до кожного відрізка [ai,bi].

Дата добавления: 2015-10-30