Формули чисельного диференціювання

Для оцінки погрішності формул квадратури необхідно обчислювати значення другої і четвертої похідної. Можна рекомендувати такі формули чисельного диференціювання:

1)Перша похідна:

а)f '(x)=[f(x+h)-f(x)]/h+O(h);

б) f '(x)=[f(x)-f(x-h)]/h+O(h);

в)f ¢(x)=[f(x+h)-f(x-h)]/(2h)+O(h²);

д)f ¢(x)=[-f(x+2h)+8f(x+h)-8f(x-h)+f(x-2h)]/(12h)+O(h⁴).

2)Друга похідна:

а)f ¢¢(x)=[f(x+h)-2f(x)+f(x-h)]/(h²)+O(h²);

б)f ¢¢(x)=[-f(x+2h)+16f(x+h)-30f(x)+16f(x-h)-f(x-2h)]/(12h²)+O(h⁴).

3)Третя похідна:

а)f ¢¢¢(x)=[f(x+2h)-2f(x+h)+2f(x-h)-f(x-2h)]/(2h³)+O(h²).

4) Четверта похідна:

а)f ¢¢¢¢(x)=[-f(x+3h)+12f(x+2h)-39f(x+h)+56f(x)-39f(x-h)+12f(x-2h)-f(x-3h)]/(6h⁴)+O(h⁴);

б)f ¢¢¢¢(x)=[f(x+2h)-4f(x+h)+6f(x)-4f(x-h)+f(x-2h)]/(h⁴)+O(h²).

Для подальшого викладу нам знадобляться відомості з теорії границь.

Означення. Назвемо величину(функцію) g(h) нескінченно малою при прямуванні h до числа а, якщо при прямуванні h до а. Найчастіше в нашому випадку а=0. Виникає потреба порівнювати нескінченно малі величини.

Наприклад, sin(h) та h прямують до нуля з однаковою швидкістю при прямуванні h до 0, а величини h²+h⁴, , sin(h³) з різною швидкістю. Для того, щоб визначити швидкість прямування до нуля цих нескінченно малих порівняємо їх з різними степенями стандартної нескінченно малої величини h: .

Очевидно, що перша функція прямує до нуля найповільніше, третя найшвидше. Введемо позначення(о маленьке та О велике): 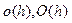. Перше (о маленьке) означає нескінченно малу величину, що прямує до нуля швидше ніж h. Тобто, якщо g(h) прямує до нуля як o(h), то це означає, що . Друге (О велике) означає, означає нескінченно малу величину, що прямує до нуля з тією швидкістю як і h.Тобто, якщо g(h) прямує до нуля як О(h), то це означає, що .

Будемо вважати, що функція f(x) має неперервну третю похідну на відрізку [x-h,x+h]. Для виводу формули чисельного диференціювання першої похідної в) можна розкласти функцію f(x+h) та f(x-h) в околі точки x:

(1)

(2)

Тут - деякі числа. Вони залежать від функції f(x), точки x та величини h. Віднявши від (1) (2), отримаємо:

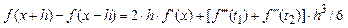, або

Якщо h прямує до нуля, то прямує до , або остаточно отримаємо

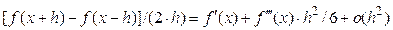. Остаточно, 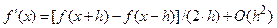(3).

Будемо вважати, що функція f(x) має неперервну четверту похідну на відрізку

[x-h,x+h]. Для виводу формули чисельного диференціювання другої похідної а) можна розкласти функцію f(x+h) та f(x-h) в околі точки x:

(4)

(5)

Тут - деякі числа. Вони залежать від функції f(x), точки x та величини h. Додамо (4) до (5) і віднімемо 2f(x) від результату:

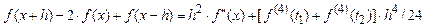, або

Якщо h прямує до нуля, то прямує до 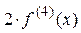: . Остаточно, 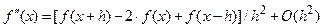(6).

Тепер виникає питання точності формул чисельного диференціювання в залежності від величини h і оптимального кроку чисельного диференціювання. Якщо б операції в формулі чисельного диференціювання виконувались б точно, то потрібно було б брати h якомога меншим. Припустимо, що похибка обчислення функції на деякому відрізку [a,b] складає відому величину, не більшу ніж e, а для всех точок відрізка [a,b]. Точніше, 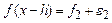. Тут наближені значення функції f(x) в точках x+h і x-h, причому . Знайдемо похибку обчислення першої похідної за формулою (3):

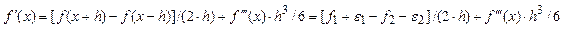. Остаточно:

Тут - сумарна похибка, вона складається з похибки обчислення функції та похибки формули (3).

. Мінімум функції T(h) можна знайти за допомогою похідної: . Мінімум досягається в точці . Тоді . Отже, існує крок чисельного диференціювання, що забезпечує мінімальну похибку.

В якості приклада розглянемо застосування формул чисельного диференціювання для знаходження першої похідної. Було перевірено чотири приклади функцій на відрізку [1,5]:

1) ln(x);

2) sin(x);

3)exp(x);

4) x⁴.

Обчислювались похідні на рівномірній сітці чисельно (PrP) - та за точними формулами(PrT), далі зна

Функция 1, номер формули 1 чисельного диференціювання:

Maxr= 4.689820E-0001 hagt= 1.000000E-0002

Maxr= 2.419672E-0001 hagt= 5.000000E-0003

Maxr= 1.229549E-0001 hagt= 2.500000E-0003

Maxr= 6.198400E-0002 hagt= 1.250000E-0003

Maxr= 3.112040E-0002 hagt= 6.250000E-0004

Maxr= 1.559252E-0002 hagt= 3.125000E-0004

Maxr= 7.804372E-0003 hagt= 1.562500E-0004

Maxr= 3.904217E-0003 hagt= 7.812500E-0005

Maxr= 1.952617E-0003 hagt= 3.906250E-0005

Maxr= 9.764354E-0004 hagt= 1.953125E-0005

Maxr= 4.882495E-0004 hagt= 9.765625E-0006

Maxr= 2.441327E-0004 hagt= 4.882813E-0006

Maxr= 1.220683E-0004 hagt= 2.441406E-0006

Maxr= 6.103488E-0005 hagt= 1.220703E-0006

Maxr= 3.051769E-0005 hagt= 6.103516E-0007

Maxr= 1.525855E-0005 hagt= 3.051758E-0007

Maxr= 7.630442E-0006 hagt= 1.525879E-0007

Maxr= 3.814930E-0006 hagt= 7.629395E-0008

Maxr= 1.911540E-0006 hagt= 3.814697E-0008

Maxr= 9.685755E-0007 hagt= 1.907349E-0008

Maxr= 5.029142E-0007 hagt= 9.536743E-0009

Maxr= 2.235174E-0007 hagt= 4.768372E-0009

Maxr= 2.235174E-0007 hagt= 2.384186E-0009

Maxr= 2.344966E-0007 hagt= 1.192092E-0009

Maxr= 7.743911E-0007 hagt= 5.960464E-0010

Maxr= 9.123160E-0007 hagt= 2.980232E-0010

Maxr= 1.724101E-0006 hagt= 1.490116E-0010

Maxr= 3.699599E-0006 hagt= 7.450581E-0011

Maxr= 7.089539E-0006 hagt= 3.725290E-0011

Maxr= 1.438930E-0005 hagt= 1.862645E-0011

Номер формулы численного дифференц 1 Minmaxr= 2.235174E-0007 hopt= 4.768372E-0009

Функция 1 порядок производной 1 номер формулы численного дифференцирования 2

Maxr= 5.360516E-0001 hagt= 1.000000E-0002

Maxr= 2.586589E-0001 hagt= 5.000000E-0003

Maxr= 1.271232E-0001 hagt= 2.500000E-0003

Maxr= 6.302577E-0002 hagt= 1.250000E-0003

Maxr= 3.138082E-0002 hagt= 6.250000E-0004

Maxr= 1.565763E-0002 hagt= 3.125000E-0004

Maxr= 7.820648E-0003 hagt= 1.562500E-0004

Maxr= 3.908286E-0003 hagt= 7.812500E-0005

Maxr= 1.953634E-0003 hagt= 3.906250E-0005

Maxr= 9.766897E-0004 hagt= 1.953125E-0005

Maxr= 4.883131E-0004 hagt= 9.765625E-0006

Maxr= 2.441486E-0004 hagt= 4.882813E-0006

Maxr= 1.220724E-0004 hagt= 2.441406E-0006

Maxr= 6.103568E-0005 hagt= 1.220703E-0006

Maxr= 3.051813E-0005 hagt= 6.103516E-0007

Maxr= 1.525972E-0005 hagt= 3.051758E-0007

Maxr= 7.631606E-0006 hagt= 1.525879E-0007

Maxr= 3.816094E-0006 hagt= 7.629395E-0008

Maxr= 1.906883E-0006 hagt= 3.814697E-0008

Maxr= 9.639189E-0007 hagt= 1.907349E-0008

Maxr= 4.749745E-0007 hagt= 9.536743E-0009

Maxr= 2.421439E-0007 hagt= 4.768372E-0009

Maxr= 2.020496E-0007 hagt= 2.384186E-0009

Maxr= 3.431960E-0007 hagt= 1.192092E-0009

Maxr= 4.005055E-0007 hagt= 5.960464E-0010

Maxr= 9.915221E-0007 hagt= 2.980232E-0010

Maxr= 2.481638E-0006 hagt= 1.490116E-0010

Maxr= 3.380738E-0006 hagt= 7.450581E-0011

Maxr= 1.142233E-0005 hagt= 3.725290E-0011

Maxr= 2.008723E-0005 hagt= 1.862645E-0011

Номер формулы численного дифференц 2 Minmaxr= 2.020496E-0007 hopt= 2.384186E-0009

Функция 1 порядок производной 1 номер формулы численного дифференцирования 3

Maxr= 3.353477E-0002 hagt= 1.000000E-0002

Maxr= 8.345856E-0003 hagt= 5.000000E-0003

Maxr= 2.084115E-0003 hagt= 2.500000E-0003

Maxr= 5.208822E-0004 hagt= 1.250000E-0003

Maxr= 1.302114E-0004 hagt= 6.250000E-0004

Maxr= 3.255227E-0005 hagt= 3.125000E-0004

Maxr= 8.138033E-0006 hagt= 1.562500E-0004

Maxr= 2.034505E-0006 hagt= 7.812500E-0005

Maxr= 5.086315E-0007 hagt= 3.906250E-0005

Maxr= 1.271610E-0007 hagt= 1.953125E-0005

Maxr= 3.180048E-0008 hagt= 9.765625E-0006

Maxr= 7.948984E-0009 hagt= 4.882813E-0006

Maxr= 2.037268E-0009 hagt= 2.441406E-0006

Maxr= 4.891270E-0010 hagt= 1.220703E-0006

Maxr= 4.984315E-0010 hagt= 6.103516E-0007

Maxr= 5.940919E-0010 hagt= 3.051758E-0007

Maxr= 1.580520E-0009 hagt= 1.525879E-0007

Maxr= 3.139547E-0009 hagt= 7.629395E-0008

Maxr= 5.591602E-0009 hagt= 3.814697E-0008

Maxr= 8.856478E-0009 hagt= 1.907349E-0008

Maxr= 1.575031E-0008 hagt= 9.536743E-0009

Maxr= 3.293270E-0008 hagt= 4.768372E-0009

Maxr= 7.412567E-0008 hagt= 2.384186E-0009

Maxr= 1.569315E-0007 hagt= 1.192092E-0009

Maxr= 4.018620E-0007 hagt= 5.960464E-0010

Maxr= 7.655642E-0007 hagt= 2.980232E-0010

Maxr= 1.283353E-0006 hagt= 1.490116E-0010

Maxr= 2.209483E-0006 hagt= 7.450581E-0011

Maxr= 5.461870E-0006 hagt= 3.725290E-0011

Maxr= 1.268649E-0005 hagt= 1.862645E-0011

Номер формулы численного дифференц 3 Minmaxr= 4.891270E-0010 hopt= 1.220703E-0006

Функция 1 порядок производной 1 номер формулы численного дифференцирования 4

Maxr= 8.295368E-0004 hagt= 1.000000E-0002

Maxr= 5.045010E-0005 hagt= 5.000000E-0003

Maxr= 3.131990E-0006 hagt= 2.500000E-0003

Maxr= 1.954216E-0007 hagt= 1.250000E-0003

Maxr= 1.220858E-0008 hagt= 6.250000E-0004

Maxr= 7.636913E-0010 hagt= 3.125000E-0004

Maxr= 4.722800E-0011 hagt= 1.562500E-0004

Maxr= 4.463985E-0012 hagt= 7.812500E-0005

Maxr= 7.011280E-0012 hagt= 3.906250E-0005

Maxr= 1.544542E-0011 hagt= 1.953125E-0005

Maxr= 2.073897E-0011 hagt= 9.765625E-0006

Maxr= 5.771206E-0011 hagt= 4.882813E-0006

Maxr= 8.555290E-0011 hagt= 2.441406E-0006

Maxr= 1.983684E-0010 hagt= 1.220703E-0006

Maxr= 5.590639E-0010 hagt= 6.103516E-0007

Maxr= 7.153584E-0010 hagt= 3.051758E-0007

Maxr= 2.065585E-0009 hagt= 1.525879E-0007

Maxr= 4.594739E-0009 hagt= 7.629395E-0008

Maxr= 8.501985E-0009 hagt= 3.814697E-0008

Maxr= 1.273698E-0008 hagt= 1.907349E-0008

Maxr= 2.157107E-0008 hagt= 9.536743E-0009

Maxr= 4.069372E-0008 hagt= 4.768372E-0009

Maxr= 1.051697E-0007 hagt= 2.384186E-0009

Maxr= 2.190197E-0007 hagt= 1.192092E-0009

Maxr= 5.881265E-0007 hagt= 5.960464E-0010

Maxr= 1.013916E-0006 hagt= 2.980232E-0010

Maxr= 1.780059E-0006 hagt= 1.490116E-0010

Maxr= 3.202478E-0006 hagt= 7.450581E-0011

Maxr= 7.448692E-0006 hagt= 3.725290E-0011

Maxr= 1.666014E-0005 hagt= 1.862645E-0011

Номер формулы численного дифференц 4 Minmaxr= 4.463985E-0012 hopt= 7.812500E-0005

Дата добавления: 2015-10-30