
Читайте также:
|
У відповідності до наближення Френеля інтеграл Френеля-Кірхгофа можна написати в наступному спрощеному вигляді:

| |
Наближення Френеля справедливо в зоні
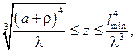
де  – максимальний радіус апертури,
– максимальний радіус апертури,  – максимальний радіус області спостереження в площині z;
– максимальний радіус області спостереження в площині z; 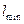 – найменша неоднорідність розподілу світлового поля
– найменша неоднорідність розподілу світлового поля  , яка зв’язана з максимальною просторовою частотою поля
, яка зв’язана з максимальною просторовою частотою поля 
Наближення Фраунгофера можна використати, якщо 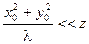 , тоді
, тоді 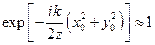 . Тоді дифракційна формула ще більше спроститься:
. Тоді дифракційна формула ще більше спроститься:
 . .
|
Якщо область, що нас цікавить, лежить в площині спостереження дифракції Фраунгофера поблизу осі 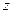 , так що виконується умова:
, так що виконується умова:
 , або
, або  , то
, то 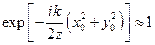 .
.
В останньому випадку наближення Фраугофера спрощується:

|
Зона дифракції Фраунгофера визначається з умови: 
Сферична лінза та її властивості
Якщо лінза достатньо тонка і міняє тільки фазу падаючого на неї світла, то комплексне пропускання  рівне:
рівне:
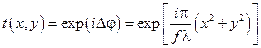 . .
|
Фокусна віддаль лінзи  зв’язана зі радіусами кривизни сферичних поверхонь
зв’язана зі радіусами кривизни сферичних поверхонь 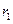 і
і  таким виразом:
таким виразом:

Якщо впритул до лінзи розміщений транспарант з комплексним пропусканням  , і на транспарант з лінзою падає плоска хвиля з амплітудою
, і на транспарант з лінзою падає плоска хвиля з амплітудою  то в задній фокальній площині
то в задній фокальній площині  лінзи матимемо розподіл амплітуд:
лінзи матимемо розподіл амплітуд:
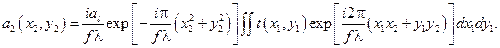
Якщо покласти  ,
,  , то останній вираз в площині
, то останній вираз в площині  можна представити так:
можна представити так:

Якщо в площині  розмістити збірну лінзу з фокусною віддалю
розмістити збірну лінзу з фокусною віддалю  то з попереднього виразу стає очевидним, що зразу за другою лінзою ми отримаємо фур’є-образ, який не містить фазового множника сферичної хвилі:
то з попереднього виразу стає очевидним, що зразу за другою лінзою ми отримаємо фур’є-образ, який не містить фазового множника сферичної хвилі:
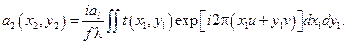
Ще одна схема може виконувати точне перетворення Фур’є у відповідності до попереднього виразу. Це коли транспарант освітлюється плоскою хвилею і розміщений в передній фокальній площині лінзи. В задній фокальній площині лінзи будемо мати розподіл амплітуд у відповідності до перетворення Фур’є.
ЗАДАЧІ
 мм розміщена ґратка з періодом
мм розміщена ґратка з періодом  мкм. Ґратка освітлюється плоскою хвилею по нормалі,
мкм. Ґратка освітлюється плоскою хвилею по нормалі,  мкм. Знайти координати яскравих піків у задній фокальній площині.
мкм. Знайти координати яскравих піків у задній фокальній площині. мм розміщена ґратка з періодом
мм розміщена ґратка з періодом  мкм. Ґратка освітлюється плоскою хвилею під кутом
мкм. Ґратка освітлюється плоскою хвилею під кутом  ,
,  мкм. Знайти координати яскравих піків у задній фокальній площині.
мкм. Знайти координати яскравих піків у задній фокальній площині. мм розміщено два взаємо когерентні джерела світла потужністю
мм розміщено два взаємо когерентні джерела світла потужністю  і
і  Ват, і які зміщені відносно осі координат оптичної системи на
Ват, і які зміщені відносно осі координат оптичної системи на  мм уверх і
мм уверх і  мм вниз. Знайти період та контраст інтерференційної картини, якщо довжина хвилі когерентних джерел складає 0.514мкм.
мм вниз. Знайти період та контраст інтерференційної картини, якщо довжина хвилі когерентних джерел складає 0.514мкм.  мкм. Плоска хвиля падає на екран по нормалі.
мкм. Плоска хвиля падає на екран по нормалі. 0мкм. Плоска хвиля падає на екран по нормалі.
0мкм. Плоска хвиля падає на екран по нормалі. мм падає плоска хвиля по нормалі
мм падає плоска хвиля по нормалі  мкм. Знайти розподіл амплітуди хвилі в області дифракції Фраунгофера на віддалі
мкм. Знайти розподіл амплітуди хвилі в області дифракції Фраунгофера на віддалі 
 мм, центри яких знаходяться на відстані
мм, центри яких знаходяться на відстані  мм, падає плоска хвиля. Описати розподіл поля в області дифракції Фраунгофера; знайти кількість періодів інтерференційної картини в межах центральної дифракційної смуги.
мм, падає плоска хвиля. Описати розподіл поля в області дифракції Фраунгофера; знайти кількість періодів інтерференційної картини в межах центральної дифракційної смуги.  мм падає плоска хвиля по нормалі
мм падає плоска хвиля по нормалі  мкм. Знайти розподіл інтенсивності в області дифракції Фраунгофера.
мкм. Знайти розподіл інтенсивності в області дифракції Фраунгофера. 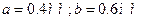 падає плоска хвиля по нормалі
падає плоска хвиля по нормалі  мкм. Знайти розподіл в області дифракції Фраунгофера. Знайти кутові координати нулів розподілу інтенсивності світла.
мкм. Знайти розподіл в області дифракції Фраунгофера. Знайти кутові координати нулів розподілу інтенсивності світла.
А)  Б)
Б) 
де 

Б)Враховуючи, що  визначити на яких відстанях
визначити на яких відстанях 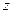 від отвору розподіл поля в площині, яка паралельна екрану, 1) модульовано в просторі тільки по амплітуді, 2) модульовано в просторі тільки по фазі?
від отвору розподіл поля в площині, яка паралельна екрану, 1) модульовано в просторі тільки по амплітуді, 2) модульовано в просторі тільки по фазі?
13. В передній фокальній площині лінзи з фокусною відстанню 300мм розміщений прямокутній отвір розмірами  мм2. Отвір освітлюється плоскою когерентною хвилею з
мм2. Отвір освітлюється плоскою когерентною хвилею з  мкм. Знайти координати точок мінімальної інтенсивності в задній фокальній площині.
мкм. Знайти координати точок мінімальної інтенсивності в задній фокальній площині.
14.В передній фокальній площині лінзи з фокусною відстанню 400мм розміщений прямокутній отвір розмірами  мм2. Отвір освітлюється плоскою когерентною хвилею з
мм2. Отвір освітлюється плоскою когерентною хвилею з  мкм. Знайти координати точок мінімальної інтенсивності в задній фокальній площині.
мкм. Знайти координати точок мінімальної інтенсивності в задній фокальній площині.
15. В передній фокальній площині лінзи з фокусною відстанню  мм розташована дифракційна ґратка з періодом
мм розташована дифракційна ґратка з періодом  мкм. Ґратка освітлюється плоскою хвилею з
мкм. Ґратка освітлюється плоскою хвилею з  мкм. Визначити координати яскравих піків в задній фокальній площині лінзи.
мкм. Визначити координати яскравих піків в задній фокальній площині лінзи.
16. В передній фокальній площині лінзи з фокусною відстанню  мм розташована двомірна дифракційна ґратка з періодом
мм розташована двомірна дифракційна ґратка з періодом  мкм у двох ортогональних напрямах. Ґратка освітлюється плоскою хвилею з
мкм у двох ортогональних напрямах. Ґратка освітлюється плоскою хвилею з  мкм. Визначити координати яскравих піків в задній фокальній площині лінзи.
мкм. Визначити координати яскравих піків в задній фокальній площині лінзи.
17. В передній фокальній площині лінзи з фокусною відстанню  мм розташована дифракційна ґратка з періодом
мм розташована дифракційна ґратка з періодом  мкм вздовж координати
мкм вздовж координати  та з періодом
та з періодом  мкм вздовж координати
мкм вздовж координати  Ґратка освітлюється плоскою хвилею з
Ґратка освітлюється плоскою хвилею з  мкм. Визначити координати яскравих піків в задній фокальній площині лінзи.
мкм. Визначити координати яскравих піків в задній фокальній площині лінзи.
18. В передній фокальній площині лінзи з фокусною відстанню  розміщено транспарант з максимальними просторовими частотами
розміщено транспарант з максимальними просторовими частотами  і
і 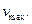 Транспарант освітлюється плоскою хвилею з
Транспарант освітлюється плоскою хвилею з  мкм. Визначити геометричні розміри світлової плями в задній фокальній площині лінзи.
мкм. Визначити геометричні розміри світлової плями в задній фокальній площині лінзи.
19. В передній фокальній площині лінзи знаходиться дифракційна ґратка, яка має 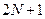 штрихів (періодів). Пропускання одного періоду описується функцією
штрихів (періодів). Пропускання одного періоду описується функцією  на інтервалі
на інтервалі 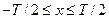 . Ґратка освітлюється плоскою хвилею з
. Ґратка освітлюється плоскою хвилею з  мкм. Знайти розподіл інтенсивності поля в задній фокальній площині. Знайти координати, ширину та відносну інтенсивність головних максимумів. Визначити координати нулів в розподілі інтенсивності та їх кількість між сусідніми головними максимумами.
мкм. Знайти розподіл інтенсивності поля в задній фокальній площині. Знайти координати, ширину та відносну інтенсивність головних максимумів. Визначити координати нулів в розподілі інтенсивності та їх кількість між сусідніми головними максимумами.
20. На рисунку наведена оптична схема, що виконує перетворення Фур'є.

Оптична схема, що виконує перетворення Фур’є з маштабуванням. S – точкове когерентне джерело світла, K – колімаційна лінза, T – транспарант або слайд, L – лінза яка виконує перетворення Фур’є, E – екран, чи фото чутливе середовище, на якому формується Фур’є спектр транспаранта (слайда)
На віддалі  перед лінзою розміщено транспарант з пропусканням
перед лінзою розміщено транспарант з пропусканням  . Точкове когерентне джерело світла розташоване на віддалі
. Точкове когерентне джерело світла розташоване на віддалі  перед транспарантом. Фокусна відстань
перед транспарантом. Фокусна відстань  довжина хвилі випромінювання джерела світла
довжина хвилі випромінювання джерела світла 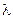 .
.
 від лінзи до екрану, на якому буде сформовано перетворення Фур’є.
від лінзи до екрану, на якому буде сформовано перетворення Фур’є.
 .
.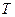 .
.
Дата добавления: 2015-10-29; просмотров: 148 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Лінійні системи | | | ЧАСТОТНИЙ АНАЛІЗ ОПТИЧНИХ СИСТЕМ |