
Читайте также:
|
При розгляді властивостей системи лінз ми будемо вважати, що всі елементи, що створюють зображення, поміщені в один “чорний ящик”, і що основні властивості системи можна повністю описати, визначаючи тільки кінцеві властивості цього пристрою. Входом цього чорного ящика є вхідна зіниця, що представляє собою отвір певних розмірів (ефективний або дійсний), через який світло повинно пройти раніше, чим воно досягне елементів, що створюють зображення, а виходом вихідна зіниця (також ефективний або дійсний), що представляє собою отвір певних розмірів, через яке світло проходить після елементів, що створюють зображення. Таким чином, розмір обох зіниць можна знайти, будуючи по законах геометричної оптики проекцію найменшої апертури системи відповідно в просторі зображень і просторі предметів. Оскільки розміри отриманих зіниць визначаються розмірами зображення ефективного отвору, існуючого десь в середині системи, вони можуть бути менші дійсних фізичних розмірів отворів у вхідній і вихідній площинах. Зауважимо, що при такому визначенні вхідна зіниця завжди є зображенням вихідної зіниці і навпаки. Оптичну систему називають дифракційно обмеженою, якщо вона перетворює сферичну хвилю, що розходиться з любого точкового джерела, в нову ідеальну сферичну хвилю, яка сходиться в точку, що лежить в площині зображення.
Амплітуду в точках зображення, що формується лінзою, в узагальненому випадку для оптичних систем представляється інтегралом суперпозиції

|
де  – амплітуда в точці площини зображення з координатами
– амплітуда в точці площини зображення з координатами  при дії точкового джерела, розміщеного в точці
при дії точкового джерела, розміщеного в точці  . У випадку відсутності аберації відгук
. У випадку відсутності аберації відгук  створюється сферичною хвилею, що сходиться, і яка іде від вихідної зіниці до точки ідеального зображення
створюється сферичною хвилею, що сходиться, і яка іде від вихідної зіниці до точки ідеального зображення  Розподіл амплітуди світла біля точки ідеального зображення представляє собою картину дифракції Фраунгофера на вихідній зіниці, центр якої (дифракції) знаходиться в точці з координатами
Розподіл амплітуди світла біля точки ідеального зображення представляє собою картину дифракції Фраунгофера на вихідній зіниці, центр якої (дифракції) знаходиться в точці з координатами  Таким чином:
Таким чином:

|
де 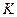 – комплексна постійна, а функція зіниці
– комплексна постійна, а функція зіниці  рівна одиниці всередині зіниці і нулю за її границею.
рівна одиниці всередині зіниці і нулю за її границею.
Ввівши ряд позначень інтеграл суперпозиції можна записати у вигляді

|
де  –ідеальне зображення в наближенні геометричної оптики, а
–ідеальне зображення в наближенні геометричної оптики, а

|
Таким чином, ми приходимо до висновку, що у випадку когерентного освітлення предмету система утворення зображення лінійна відносно комплексної амплітуди.
Якщо освітлення предмету абсолютно некогерентне, тоді інтенсивність вихідного зображення можна описати наступним чином:
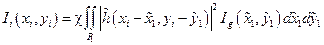 . .
|
Інтенсивність зображення визначається як згортка ідеальної інтенсивності  і імпульсного відгуку
і імпульсного відгуку  . У випадку некогерентного освітлення предмету оптичну систему потрібно розглядати як лінійне перетворення інтенсивності. Крім цього, імпульсний відгук пропорційний квадрату модуля імпульсного відгуку, який отримується при когерентному освітленні.
. У випадку некогерентного освітлення предмету оптичну систему потрібно розглядати як лінійне перетворення інтенсивності. Крім цього, імпульсний відгук пропорційний квадрату модуля імпульсного відгуку, який отримується при когерентному освітленні.
Якщо взяти перетворення Фур’є від інтегралу суперпозиції, який представлений інтегралом згортки ідеального зображення  та імпульсного відгуку
та імпульсного відгуку  , то отримаємо:
, то отримаємо:


 ,
, 
Функцію  будемо називати когерентною передавальною функцією, яка визначається вихідною зіницею. Отже для дифракційно обмеженої системи
будемо називати когерентною передавальною функцією, яка визначається вихідною зіницею. Отже для дифракційно обмеженої системи
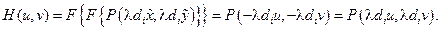
|
Тому що функція зіниці Р завжди рівна або одиниці або нулю, те саме справедливо для когерентної передавальної функції. Це, природно, означає, що в частотній області дифракційно обмежена система має обмежену смугу пропускання, всередині якої всі частотні складові пропускаються без спотворення амплітуди і фази. На границі цієї смуги пропускання частотний відгук зразу падає до нуля, в силу чого частотні складові поза смугою пропускання повністю відсутні.
Нормовану передавальну функцію оптичної некогерентної системи можна визначити таким чином:

|
Функція  відома під назвою оптична передавальна функція (скорочено ОПФ) системи. Її модуль
відома під назвою оптична передавальна функція (скорочено ОПФ) системи. Її модуль  називають модуляційна передавальна функція (МПФ). Функція
називають модуляційна передавальна функція (МПФ). Функція  зв’язана передавальною функцією
зв’язана передавальною функцією  когерентної оптичної системи таким чином:
когерентної оптичної системи таким чином:

|
Останній вираз визначає основний зв’язок між властивостями когерентних та некогерентних систем. Замітимо, що воно повністю справедливе для систем як з абераціями так і для систем без аберацій. Найважливіші властивості ОПФ:

Для когерентної системи  . Таким чином для некогерентної системи, з простою заміною змінних, маємо
. Таким чином для некогерентної системи, з простою заміною змінних, маємо

|
Останній вираз для N допускає надзвичайно важливу геометричну інтерпретацію. Чисельник представляє область перекриття двох зміщених функцій зіниці, центр однієї із яких лежить в точці з координатами  а центр другої — в діаметрально протилежній точці
а центр другої — в діаметрально протилежній точці  Знаменник просто нормує цю область перекриття до повної площі зіниці. Таким чином
Знаменник просто нормує цю область перекриття до повної площі зіниці. Таким чином

Якщо в системі присутні аберації, то їх можна врахувати у вигляді фазової помилки в точці  вихідної зіниці, як
вихідної зіниці, як  , де
, де  , а
, а  – ефективна похибка довжини шляху. Комплексний коефіцієнт пропускання
– ефективна похибка довжини шляху. Комплексний коефіцієнт пропускання  вихідної зіниці можна представити у вигляді:
вихідної зіниці можна представити у вигляді:

|
Комплексну функцію  можна вважати узагальненою функцією зіниці. Імпульсний відклик когерентної системи з абераціями представляє собою просто картину дифракції Фраунгофера на отворі з коефіцієнтом пропускання
можна вважати узагальненою функцією зіниці. Імпульсний відклик когерентної системи з абераціями представляє собою просто картину дифракції Фраунгофера на отворі з коефіцієнтом пропускання  .Імпульсний відклик некогерентної системи з абераціями рівний квадрату модуля імпульсного відклику когерентної системи. Таким чином, передавальна функція при когерентному освітленні запишемо наступним чином:
.Імпульсний відклик некогерентної системи з абераціями рівний квадрату модуля імпульсного відклику когерентної системи. Таким чином, передавальна функція при когерентному освітленні запишемо наступним чином:
 .
.
Очевидно, що у випадку когерентного освітлення обмеження смуги пропускання передавальної функції, яке зумовлене кінцевими розмірами вихідної зіниці, не залежить від наявності аберацій. Аберації вносять лише фазові спотворення в межах смуги пропускання.
Вплив аберацій на ОПФ є складнішим. Для спрощення позначень введемо функцію  , яка визначається як область перекриття функцій
, яка визначається як область перекриття функцій
 і
і 
Таким чином, ОПФ дифракційно обмеженої системи в нових позначеннях має вигляд:

Цей вираз дозволяє нам безпосередньо пов’язати похибку хвильового фронту і ОПФ. Як важливу загальну властивість, необхідно відмітити той факт, що аберації ніколи не збільшують МПФ(модуль ОПФ). Аберації будуть в основному зменшувати контраст кожної просторово-частотної складової інтенсивності зображення. Абсолютне значення граничної частоти залишається незмінним, але сильні аберації будуть настільки зменшувати високочастотні складові ОПФ, що ефективна гранична частота буде набагато менша відповідної величини в дифракційно обмеженій системі. Крім цього аберація може привести до від’ємних значень ОПФ в деяких діапазонах частот, що зовсім неможливо в системах вільних від аберацій. Якщо ОПФ від’ємна, то складові зображення на цих частотах підлягають реверсу контрасту, тобто піки інтенсивності перетворюються в нулі інтенсивності і навпаки.
ЗАДАЧІ
 лінзи з фокусною відстанню
лінзи з фокусною відстанню  Визначити діаметр та розташування вхідної та вихідної зіниць оптичної системи.
Визначити діаметр та розташування вхідної та вихідної зіниць оптичної системи. розташована на віддалі
розташована на віддалі  перед лінзою з фокусною відстанню
перед лінзою з фокусною відстанню  Визначити діаметр та розташування вхідної та вихідної зіниць оптичної системи.
Визначити діаметр та розташування вхідної та вихідної зіниць оптичної системи.  мм розташована на віддалі
мм розташована на віддалі  мм після лінзи з фокусною відстанню
мм після лінзи з фокусною відстанню  мм. Предметна площина розташована перед лінзою на відстані
мм. Предметна площина розташована перед лінзою на відстані  мм. Визначити діаметр та розташування вихідної зіниці та відстань від вихідної зіниці до площини формування зображення оптичної системи.
мм. Визначити діаметр та розташування вихідної зіниці та відстань від вихідної зіниці до площини формування зображення оптичної системи. 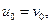 якщо
якщо  мкм.
мкм.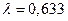 мкм.
мкм. мм, а відстань від вихідної зіниці до площини формування зображення 120мм,
мм, а відстань від вихідної зіниці до площини формування зображення 120мм, 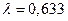 мкм.
мкм. мм2, а відстань від вихідної зіниці до площини формування зображення 100мм,
мм2, а відстань від вихідної зіниці до площини формування зображення 100мм,  мкм.
мкм. мм2, а відстань від вихідної зіниці до площини формування зображення 100мм,
мм2, а відстань від вихідної зіниці до площини формування зображення 100мм,  мкм.
мкм.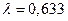 мкм.
мкм. мм2, а відстань від вихідної зіниці до площини формування зображення 100мм,
мм2, а відстань від вихідної зіниці до площини формування зображення 100мм,  мкм.
мкм. мм2, а відстань від вихідної зіниці до площини формування зображення 100мм, довжина хвилі рівна 0,670мкм.
мм2, а відстань від вихідної зіниці до площини формування зображення 100мм, довжина хвилі рівна 0,670мкм. мм,
мм,  мм, а відстань від предметної площини до лінзи складає 120 мм,
мм, а відстань від предметної площини до лінзи складає 120 мм,  мкм.
мкм. мм,
мм,  мм,
мм,  мм, а відстань від предметної площини до лінзи складає 120 мм,
мм, а відстань від предметної площини до лінзи складає 120 мм,  мкм.
мкм. мм,
мм,  мм,
мм,  мм, а відстань від предметної площини до лінзи складає 120 мм,
мм, а відстань від предметної площини до лінзи складає 120 мм,  мкм.
мкм. мм,
мм,  мм, а відстань від предметної площини до лінзи складає 120 мм,
мм, а відстань від предметної площини до лінзи складає 120 мм,  мкм.
мкм. мм,
мм,  мм,
мм,  мм, а відстань від предметної площини до лінзи складає 120 мм,
мм, а відстань від предметної площини до лінзи складає 120 мм,  мкм.
мкм. мм,
мм,  мм,
мм,  мм, а відстань від предметної площини до лінзи складає 120 мм,
мм, а відстань від предметної площини до лінзи складає 120 мм,  мкм.
мкм.Таблиця 1
 , нм , нм
| d0, мм | d1, мм | d2, мм | f1, мм | f2, мм | D, мм |
| 514 | 30 | 35 | 50 | 20 | 30 | 7 |

С – предметна площина, S – джерело світла, К – колімуюча лінза, А – реальна зіниця, L1 і L2 – система лінз, що формують зображення, Е – екран, на якому формується зображення.
21.Некогерентна оптична система має зіницю у вигляді квадрату зі стороною 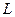 . Квадратний непропускаючий екран з стороною
. Квадратний непропускаючий екран з стороною  (див. рис.1) розміщений у центрі зіниці.
(див. рис.1) розміщений у центрі зіниці.
а) Побудувати графік ОПФ при наявності та відсутності екрану.
б) Побудувати графік ОПФ в граничному випадку, коли розмір екрану дещо менший розміру квадратної зіниці  .
.
22.Зображення предмету з амплітудним коефіцієнтом пропускання у вигляді “прямокутної хвилі”  утворюється при допомозі лінзи, що має круглу зіницю. Фокусна відстань лінзи рівна 10 см. Частота першої гармоніки прямокутної хвилі рівна 100 періодів/мм. Віддаль до предметної площини рівна 20см, довжина хвилі світла 10-4 см. Знайти мінімальний діаметр лінзи, при якому буде ще замітна деяка зміна інтенсивності в площині зображення для випадків: а) когерентне освітлення предмету; б)некогерентне освітлення предмету.
утворюється при допомозі лінзи, що має круглу зіницю. Фокусна відстань лінзи рівна 10 см. Частота першої гармоніки прямокутної хвилі рівна 100 періодів/мм. Віддаль до предметної площини рівна 20см, довжина хвилі світла 10-4 см. Знайти мінімальний діаметр лінзи, при якому буде ще замітна деяка зміна інтенсивності в площині зображення для випадків: а) когерентне освітлення предмету; б)некогерентне освітлення предмету.
23. Синусоїдальний тест-об’єкт з амплітудним коефіцієнтом пропускання  розміщена перед оптичною системою. Допускаючи, що частота достатньо мала, для того, щоб була пропущена системою, а збільшення системи рівне одиниці: а) знайти розподіл інтенсивності в площині зображення для системи вільної від аберацій; Показати, що цей самий розподіл інтенсивності утворюється в нескінченній множині площин простору зображення, які відмінні від площини фокусування.
розміщена перед оптичною системою. Допускаючи, що частота достатньо мала, для того, щоб була пропущена системою, а збільшення системи рівне одиниці: а) знайти розподіл інтенсивності в площині зображення для системи вільної від аберацій; Показати, що цей самий розподіл інтенсивності утворюється в нескінченній множині площин простору зображення, які відмінні від площини фокусування.
Дата добавления: 2015-10-29; просмотров: 117 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дифракційні формули Френеля і Фраунгофера | | | Розширення та фільтрація лазерного пучка |