
Читайте также:
|
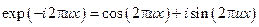 і використати симетричність функції
і використати симетричність функції 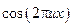 і анти симетричність
і анти симетричність 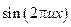 .
.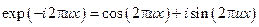 і використати симетричність функції
і використати симетричність функції 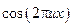 і анти симетричність
і анти симетричність 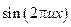 .
.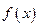 інтеграл взяти один раз по частинах.
інтеграл взяти один раз по частинах.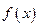 інтеграл взяти два рази по частинах.
інтеграл взяти два рази по частинах.15. 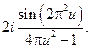
16. 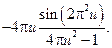
17. 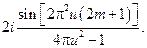
18. 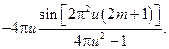
19. 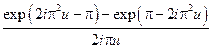 .
.
20. 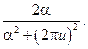
21. 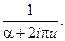
22. 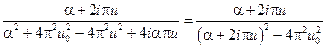 .
.
23. 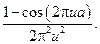
24. 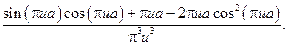
25. 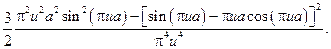
26. 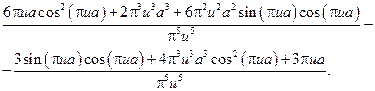
27.1.У задачах 27.1-6 скористатись результатами задач 3 і 4. У задачі 27.1 використати розв’язок задачі 24.
27.2. У задачі 27.2 використати розв’язок задачі 26.
27.3. У задачі 27.3 використати розв’язок задачі 23.
27.4. У задачі 27.4 використати розв’язок задачі 25.
27.5. У задачі 27.5 використати розв’язок задачі 8.
21.6. У задачі 27.6 використати розв’язок задачі 9.
28. Вказівка: Знайти перетворення Фур’є від функції 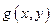 та покласти, що
та покласти, що 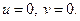 Відповідно знайти обернене перетворення Фур’є від
Відповідно знайти обернене перетворення Фур’є від 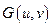 та покласти, що
та покласти, що 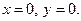
29. 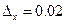 мм.
мм.
30. 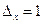 мм.
мм.
31. 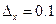 мм.
мм.
32. Фур'є-образ 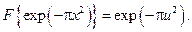 Максимальне значення фур'є-образу складає 1.0. Приймемо
Максимальне значення фур'є-образу складає 1.0. Приймемо 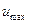 таким чином, щоб
таким чином, щоб 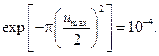 Звідси
Звідси 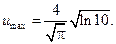 Отже
Отже 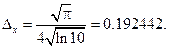
33. Якщо вибраний максимально допустимий інтервал відліків 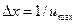 , то справедливий вираз
, то справедливий вираз
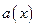 =
= 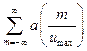
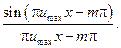
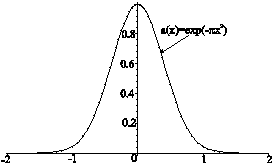
На рис.1 наведено функцію 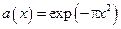 і функції
і функції 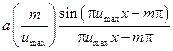 для
для  : при цьому
: при цьому 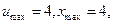
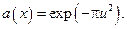
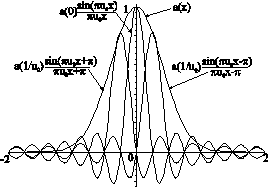
|
Рис.1 Відновлення вихідної функції 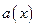 за відліками функції за відліками функції 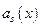 в просторовій області. в просторовій області.
|
Тобто функцію 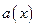 можна відновити з допомогою відліків цієї функції в дискретних точках і функції
можна відновити з допомогою відліків цієї функції в дискретних точках і функції 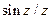 . Слід відзначити, що вираз
. Слід відзначити, що вираз 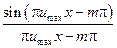 приймає одиницю для
приймає одиницю для  - відліку,
- відліку, 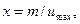 і рівний нулю для всіх інших позицій. Якщо врахувати всі члени суми, рахуючи як позитивний центральний максимум, так і позитивні і від’ємні бокові максимуми, то можна точно відновити неперервну функцію
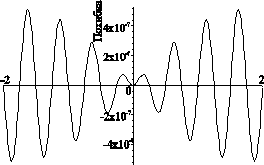
і рівний нулю для всіх інших позицій. Якщо врахувати всі члени суми, рахуючи як позитивний центральний максимум, так і позитивні і від’ємні бокові максимуми, то можна точно відновити неперервну функцію 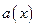 , що наведено на рис.2.
, що наведено на рис.2.
34. Фур'є-образ 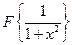 не виражається через елементарні функції. Тому потрібно побудувати графік
не виражається через елементарні функції. Тому потрібно побудувати графік 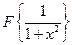 як функція частоти. Якщо
як функція частоти. Якщо 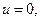 то фур'є-образ на цій частоті рівний
то фур'є-образ на цій частоті рівний 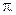 З графіка
З графіка 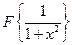 можна переконатись, що на частоті
можна переконатись, що на частоті 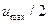 =1.4659 фур'є-образ рівний
=1.4659 фур'є-образ рівний 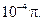 Отже
Отже 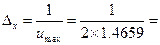 0.3411.
0.3411.
| 
|
| а) | б) |
Рис.2а. Неперервна функція – 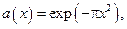 крапки – відновлена функція за відліками, крапки – відновлена функція за відліками, 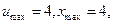  у сумі міняється від у сумі міняється від  до до 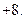
| Рис.2б. Різниця між 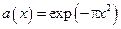 і відновленою функцією за її відліками для даних, що наведені у підписі до рис. 2а. і відновленою функцією за її відліками для даних, що наведені у підписі до рис. 2а.
|
35. Поступаємо, як в задачі 33. Для функції 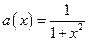 візьмемо
візьмемо 
 у сумі міняється від
у сумі міняється від 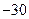 до
до 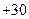
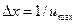 . Скористаємось виразом
. Скористаємось виразом 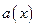 =
= 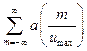
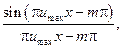 та
та 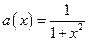 . Знайдемо похибку у відновленні функції за її відліками. Сама відновлена функція та похибка у відновленні представлена на рис.3.
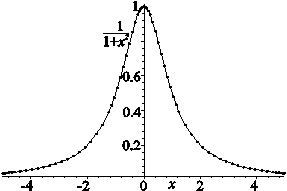
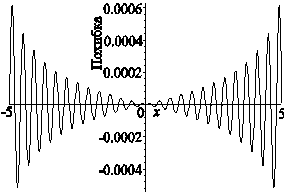
. Знайдемо похибку у відновленні функції за її відліками. Сама відновлена функція та похибка у відновленні представлена на рис.3.
| 
|
| а) | б) |
Рис.3а. Неперервна функція 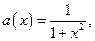 крапки – відновлена функція за відліками, крапки – відновлена функція за відліками, 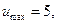 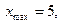  у сумі міняється від у сумі міняється від 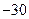 до до 
| Рис.3б Різниця між 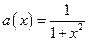 і відновленою функцією за її відліками для даних, що наведені у підписі до рис. 3а. і відновленою функцією за її відліками для даних, що наведені у підписі до рис. 3а.
|
Дана функція 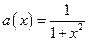 не так швидко прямує до нуля як
не так швидко прямує до нуля як 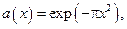 тому для точного відновлення потрібно брати більше відліків, в даному випадку
тому для точного відновлення потрібно брати більше відліків, в даному випадку  у сумі міняється від
у сумі міняється від 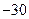 до
до 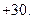
41. 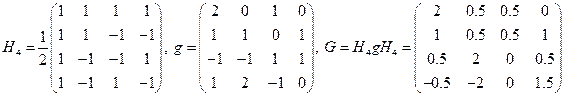 .
.
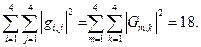
Задачі 42, 43, 44 зробити таким же чином як задачу 41.
45. 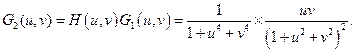
46. 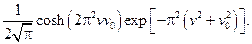
47. 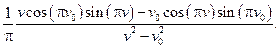
48, 49, 50. Вказівка: Задачі 48, 49, 50 виконати на комп’ютері за допомогою програмного забезпечення, яке виконує перетворення Фур’є або інтегрування в символічній формі, наприклад в Maple.
Дата добавления: 2015-10-29; просмотров: 122 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод фазового контрасту | | | Поширення світла та його дифракція |