Поширення світла та його дифракція

1. Координати дифракційних максимумів можна визначити за виразом:

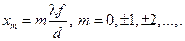Для даної задачі мм

1. Кут повинен вимірюватись в радіанах.

1. Розподіл інтенсивності визначається виразом: Період інтерференційної картини 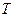розрахуємо за формулою: 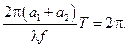Звідси мкм. Контраст інтерференційної картини можна визначити за виразом:
2. Див. конспект лекцій.
3. Див. конспект лекцій.

6. Розподіл інтенсивності на віддалі від щілини можна описати виразом:

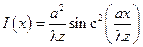. Ширину центральної смуги 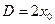у області дифракції Фраунгофера на екрані можна визначити з виразу 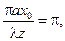отже

1. Розподіл інтенсивності на віддалі від двох щілин можна описати виразом: Звідси період інтерференційної картини рівний: Таким чином кількість інтерференційних смуг, що покривають центральну дифракційну смугу можна визначити за виразом:
2. Розподіл інтенсивності на віддалі від круглого отвору описується виразом: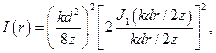

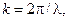
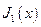– функція Бесселя першого порядку. Цей розподіл здебільшого називають картиною Ері. Радіус першого темного кола визначається виразом: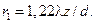

9. Лінійні координати нулів можна визначити з виразів: 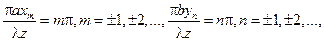. Звідси кутові координати нулів рівні:

10.Амплітуду хвилі в області дифракції Фраунгофера (площина ) можна виразити як різницю розподілів на двох квадратних отворах розмірами 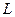і Отже будемо мати: , Відповідно, розподіл інтенсивності матиме вигляд:

.

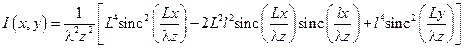11. А) Розподіл амплітуди на осі оптичної системи 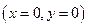згідно дифракційної формули Френеля можна записати наступним чином:

або в полярній системі координат:

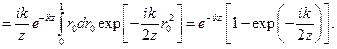
Розподіл інтенсивності на осі матиме вид: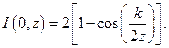

Б) В даному випадку маємо прозоре кільце, на якому дифрагує світло. Використовуючи розв’язок задачі А), можемо написати, що амплітуда хвилі на оптичній осі рівна:

Отже інтенсивність

12. Розподіл амплітуди хвилі на віддалі від екрану матиме вигляд:

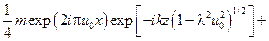
+ . Розподіл поля буде модульований по амплітуді для тих площин, для яких виконується умова: або Якщо –парне число, то відтвориться амплітудна ґратка, якщо – не парне число, то відтвориться ґратка з протилежним контрастом до вихідної. Таке оптичне явище відтворення ґратки називається ефектом Тальбота.

Б)Якщо 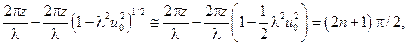тобто відтвориться фазова ґратка на відстані

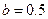13. Для розв’язку цієї задачі скористаємось виразом: , де мм, мм,

14. Хід розв’язку задачі аналогічний розв’язку задачі 13.

15.В параксіальному наближенні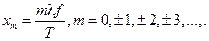

16.

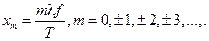
17.

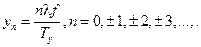
18. розміри світлової плями рівні:

19. Вказівка: Знайти перетворення Фур’є одного штриха ґратки і використати теорему про зміщення. Потім знайти суму геометричної прогресії, яка має членів. Кількість нулів між сусідніми головними максимумами рівна

20. Вказівка: Використати матеріали конспекту.

Дата добавления: 2015-10-29