
Чисельне інтегрування
1)Задача інтегрування неперервної функції легко розв'язується аналітично, якщо відома її первісна F (x). Визначений інтеграл від цієї функції може бути обчислений по формулі Ньютона - Лейбніца: 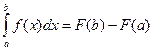 , де F¢(x) =f(x).
, де F¢(x) =f(x).
Проте у багатьох випадках первісна F(x) не може бути виражена за допомогою елементарних функцій або є дуже складною. Тому обчислення визначеного інтеграла по формулі Ньютона-Лейбніца може бути нездійсненним або важким.
Наприклад, - інтеграл, що не береться в елементарних функціях.
Наближене обчислення інтегралів  , полягає заміні визначеного інтеграла скінечною сумою
, полягає заміні визначеного інтеграла скінечною сумою  , де Сk числові коефіцієнти і xk - деякі точки, k=0, 1,…,n.
, де Сk числові коефіцієнти і xk - деякі точки, k=0, 1,…,n.
Означення 1. Наближена рівність називається квадратурною формулою. Точки xk називаються вузлами квадратурної формули. Різниця називається похибкою квадратурної формули.
Слід помітити, що в більш загальному означенні квадратурної формули в суму можуть входити не тільки значення функції, але і значення першої похідної.
Похибка залежить від функції f, відрізка інтегрування, від розташування вузлів і вибору коефіцієнтів квадратурної формули. Вузли квадратурної формули можуть належати до відрізка інтегрування, а можуть і не належати. Наближене інтегрування може бути виконане з будь-якою точністю.
Означення 2. Для зниження похибки чисельного інтегрування відрізок [а,b] розібємо на сукупність малих відрізків [xi-1,xi], таких, що. Представимо інтеграл у вигляді суми інтегралів по часткових відрізках:.
Така формула чисельного інтегрування називається складеною.
Формула трапецій
1)Замінимо функцію f(х) на відрізку [xi-1,xi] інтерполяційним поліномом Лагранжа першого степеня. Позначимо yi=f(xi), yi-1=f(xi-1), h= xi-xi-1. Інтерполяційний поліном Лагранжа першого степеня для двох точок:P1(x)=yi-1L1(x)+ yiL2(x).
Для L1(x)=(x-xi)/(xi-1-xi)=(xi-x)/h, L2(x)=(x-xi-1)/(xi-xi-1)=(x-xi-1)/h.
Похибка: R(x)=(x-xi-1)(x-xi)*f"(t)/2, де xi-1≤ t ≤ xi.
Тоді f(х)=P1(x)+R(x)= [yi-1(xi-x)+ yi (x-xi-1)]/h+f ¢¢(e)(x-xi)(x-xi-1)/2, де точка eÎ[xi-1,xi].

Обчислимо інтеграл I1:
 Обчислимо інтеграл I2:
Обчислимо інтеграл I2:

Остатоточно,.
Оцінимо тепер інтеграл I3.
Припустимо, що модуль другої похідної від функції f обмежений на відрізку [а,b]: |f ²(x)|<M, при всіх х, що належать відрізку [а,b].
Тепер можна оцінити інтеграл I3 (похибку): 
| I3|=|  |/2<
|/2< 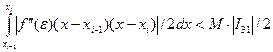 , де
, де  або
або

Отже, 
Дата добавления: 2015-10-30; просмотров: 100 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Подальший розвиток умов для підприємництва | | | Автоматичний вибір кроку інтегрування |