Інтегрування ірраціональних функцій. Інтеграли, що містять .

Розглянемо інтеграли вигляду:

, ,

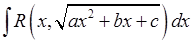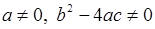де – раціональна функція змінних 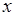та 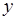. Такі інтеграли можна звести до інтегралів від раціональних функцій за допомогою підстановок Ейлера:

1) , якщо ,

2) , якщо ,

3) , якщо .

У 3-му випадку 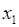– один з коренів квадратного тричлена . Знак «плюс» чи «мінус» в цих підстановках обирається в залежності від конкретного вигляду підінтегральної функції з огляду на те, щоб підінтегральна функція, яка отримується внаслідок підстановки, була якомога простішою. Слід, тем не менш, відмітити, що, як правило, підстановки Ейлера приводять до громіздких обчислень.

Приклади.

1. .

Зробимо підстановку: . Тоді, розв’язуючи відносно 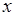ірраціональне рівняння, дістанемо:

, .

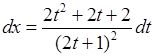Підставляючи під знак інтегралу, отримаємо інтеграл від раціональної функції:

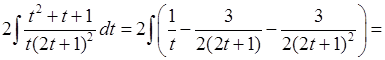
(розкладання підінтегрального дробу на елементарні та знаходження невизначених коефіцієнтів виконайте самостійно). Для отримання остаточної відповіді залишилося тільки в останній вираз підставити вираз для .

2. .

Зробимо підстановку: . Тоді:

, .

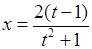Підставляючи під знак інтеграла, дістаємо:

.

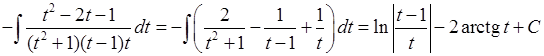Повертаючись до змінної 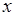за формулою 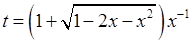, отримаємо остаточну відповідь.

3. .

Враховуючи те, що квадратний тричлен під знаком квадратного кореня має додатний дискримінант, і один з коренів цього тричлена , здійснимо підстановку:

.

Тоді, розв’язуючи ірраціональне рівняння відносно 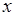, знайдемо два його кореня:

, .

Зрозуміло, що перший з цих коренів обирати нема сенсу, тому:

, , .

Підставляючи під знак інтеграла, отримуємо інтеграл від раціональної функції:

.

Самостійно переконайтеся у тому, що цей інтеграл дорівнює:

.

Розглянемо тепер інтеграл вигляду:

, (11.1) де – многочлен степеня . Покажемо, що цей інтеграл можна подати у вигляді:

, (11.2)

де – многочлен степеня з невизначеними коефіцієнтами, а 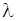– поки що також невизначене число. Диференцюючи тотожність (11.2), і, домножаючи після цього обидві частини рівності на , дістанемо:

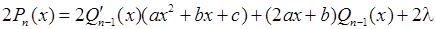. (11.3)

Зрівнюючи в (11.3) коефіцієнти при однакових степенях 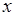у лівій та правій частинах, визначимо коефіцієнти многочлена і число 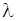. Інтеграл в правій частині формули (11.2) відноситься до типу, який розглянуто в п. 6.

Інтеграли вигляду

, де , зводяться до інтегралу вигляду (11.1) підстановкою:

.

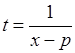Приклади.

1. .

Згідно з формулою (11.2) маємо:

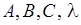, (11.4) де коефіцієнти підлягають визначенню. Рівність (11.3) у даному випадку набуває вигляду:

.

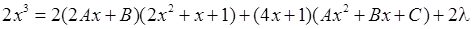Розкриваючи дужки та зрівнюючи коефіцієнти при 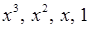, отримаємо наступну систему відносно :

,

,

,

.

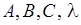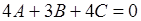Розв’язуючи цю систему, отримуємо:

.

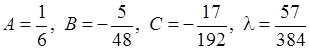Обчислимо тепер:

.

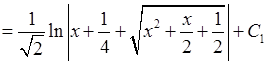Підставляючи тепер до (11.4), дістаємо:

.

2.

.

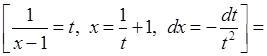
Дата добавления: 2015-10-30